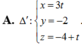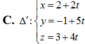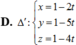Trong không gian Oxyz, cho đường thẳng d : x - 1 1 = y - 2 2 = z - 3 1 và mặt phẳng α : x + y + z - 2 = 0 Đường thẳng nằm trong mặt phẳng α , đồng thời vuông góc và cắt đườn thẳng d có phương trình là
A. ∆ 3 : x - 3 3 = y - 2 - 2 = z - 5 1
B. ∆ 1 : x + 2 - 3 = y + 4 2 = z + 4 3
C. ∆ 2 : x - 22 1 = y - 4 - 2 = z - 4 3
D. ∆ 2 : x - 1 3 = y - 1 - 2 = z 1
Đường thẳng d đi qua điểm A(1;2;3) và có vectơ chỉ phương u ⇀ = ( 1 ; 2 ; 1 )
- Mặt phẳng (P) có vectơ pháp tuyến n ⇀ = ( 1 ; 1 ; - 1 )
- Gọị B là giao điểm của đườn thẳng d và mặt phẳng (P) cho B(2;4;4)
- Vì đường thẳng cần tìm ∆ nằm trong mặt phẳng α , đồng thời vuông góc và cắt đường thẳng d cho nên đường thẳng ∆ đi qua điểm B(2;4;4) và có vectơ chỉ phương
u ∆ ⇀ = u ⇀ ; n ⇀ = ( - 3 ; 2 ; - 1 ) ⇒ x = 2 - 3 t y = 4 + 2 t z = 4 - t
- Đối chiếu đáp án ta thấy đường thẳng
∆
3
của đáp án A có cùng véctơ chỉ phương và đi qua điểm
M(5;2;5) thuộc
∆
:
⇒
x
=
2
-
3
t
y
=
4
+
2
t
z
=
4
-
t
Chọn đáp án A.