Chọn A
Mặt phẳng (P) cắt các tia Ox, Oy, Oz lần lượt tại A, B, C nên A (a;0;0), B (0;b;0), C (0;0;c) (a, b, c>0).
Phương trình mặt phẳng 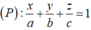
+ Mặt phẳng (P) qua M nên ![]()
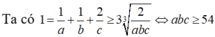
+ Thể tích khối tứ diện OABC: ![]()
Thể tích khối tứ diện OABC nhỏ nhất khi 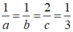 suy ra a=3, b=3, c=6.
suy ra a=3, b=3, c=6.
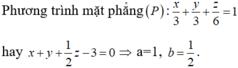
Vậy S = 0

