Đáp án D
Phương pháp: Sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng.
Cách giải:
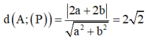
![]()
![]()
Đáp án D
Phương pháp: Sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng.
Cách giải:
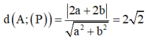
![]()
![]()
Trong không gian Oxyz, cho ba điểm thay đổi A(a; 0; 0), B(0; b; 0), C(0; 0; c) trong đó a, b, c khác 0 và thỏa mãn điều kiện 3ab + bc - 2ac = abc . Khoảng cách lớn nhất từ O đến mặt phẳng (ABC) là:
A. 14
B. 14
C. 1/ 14
D. Không tồn tại
Trong không gian với hệ tọa độ Oxyz, cho các điểm . Khẳng A(1;2;2), B(2;1;3), C(3;0;4) định nào sau đây là đúng?
A. A,B,C thẳng hàng
B. A,B,C tạo thành tam giác cân tại A
C. A,B,C tạo thành tam giác đều
D. A,B,C tạo thành tam giác vuông
Trong không gian tọa độ Oxyz, cho hai điểm A ( 1 ; 0 ; 0 ) , B ( 5 ; 0 ; 0 ) . Gọi (H) là tập hợp các điểm M trong không gian thỏa mãn M A → . M B → = 0 . Khẳng định nào sau đây là đúng?
A. (H) là một đường tròn có bán kính bằng 4
B. (H) là một mặt cầu có bán kính bằng 4
C. (H) là một đường tròn có bán kính bằng 2
D. (H) là một mặt cầu có bán kính bằng 2
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-1; 2; 4) và B (0; 1; 5). Gọi (P) là mặt phẳng đi qua A sao cho khoảng cách từ B đến (P) là lớn nhất. Khi đó, khoảng cách d từ O đến mặt phẳng (P) bằng bao nhiêu?
A . d = - 3 3
B . d = 3
C . d = 1 3
D . d = 1 3
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y + 2 1 = z - 1 2
và d 2 : x - 1 2 = y - 1 1 = z + 2 1 . Mặt phẳng (P) : x + ay + bz + c = 0 song song
với d 1 , d 2 và khoảng cách từ d 1 đến (P) bằng 2 lần khoảng cách từ d 2 đến (P).
Giá trị của a + b + c bằng
A. 6
B. 14
C. -4
D. -6
Trong không gian Oxyz, mặt phẳng qua ba điểm A(1;3;2), B(2;5;9), C(-3;7;-2) có phương trình là 3x+ay+bz+c=0. Giá trị a+b+c bằng
A. -6.
B. 3.
C. -3.
D. 6.
Trong không gian tọa độ Oxyz, cho điểm A(a;b;c) với a , b , c ∈ ℝ \ 0 . Xét (P) là mặt phẳng thay đổi đi qua điểm A. Khoảng cách lớn nhất từ điểm O đến mặt phẳng (P) bằng
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi tùy ý sao cho a 2 + b 2 + c 2 = 3 . Khoảng cách từ O đến mặt phẳng (ABC) lớn nhất bằng
A. 1 3
B. 3
C. 1 3
D. 1
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A (1;-3;2), B (3;5;-2). Phương trình mặt phẳng trung
trực của AB có dạng x + ay + bz + c =0.
Khi đó a + b + c bằng
![]()
![]()
![]()
![]()