Chọn D
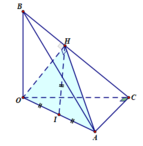
+) Dễ thấy B ∈ Oz . Ta có A ∈ (Oxy) và C ∈ (Oxy), suy ra OB ⊥ (OAC)
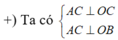
![]()
![]()
![]()
Từ (1) và (2) suy ra
![]()
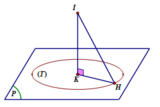
+) Với OH ⊥ AB suy ra H thuộc mặt phẳng (P) với (P) là mặt phẳng đi qua O và vuông góc với đường thẳng AB. Phương trình của (P) là: y-z=0.
+) Với OH ⊥ HA => tam giác OHA vuông tại H. Do đó H thuộc mặt cầu (S) có tâm I(0;2 2 ;0) là trung điểm của OA và bán kính R = O A 2 = 2 2
+) Do đó điểm H luôn thuộc đường tròn (T) cố định là giao tuyến của mặt phẳng (P) với mặt cầu (S).
+) Giả sử (T) có tâm K và bán kính r thì
![]()
Vậy điểm H luôn thuộc đường tròn cố định có bán kính bằng 2.

