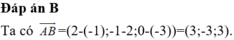Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho véc-tơ (1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ ?
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho véc-tơ ![]() =(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ
=(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ ![]() ?
?
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(0;3;-2) và N(2;-1;0). Tọa độ của véc tơ
M
N
→
là: A. (2;-4;2) B. (1;1;-1) C. (-2;4;-2) D. (2;2;-2)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(0;3;-2) và N(2;-1;0). Tọa độ của véc tơ M N → là:
A. (2;-4;2)
B. (1;1;-1)
C. (-2;4;-2)
D. (2;2;-2)
Trong không gian với hệ tọa độ Oxyz, cho hai véc tơ
a
→
1
;
-
1
;
2
và
b
→
2
;
1
;
-
1
Tính
a
→
....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai véc tơ a → = 1 ; - 1 ; 2 và b → = 2 ; 1 ; - 1 Tính a → . b →
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ . Tìm tọa độ điểm A. A. A(-2;3;0) B. A(-2;0;3) C. A(0;2;-3) D. A(0;-2;3).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ ![]() . Tìm tọa độ điểm A.
. Tìm tọa độ điểm A.
A. A(-2;3;0)
B. A(-2;0;3)
C. A(0;2;-3)
D. A(0;-2;3).
Trong không gian với hệ tọa độ Oxyz, cho véc tơ
u
→
(
1
;
1
;
-
2
)
,
v
→
(
1
;
0
;
m
)
. Tìm tất c giá trị của m để góc giữa
u
→
,
v
→
bằng 45
°
.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho véc tơ u → = ( 1 ; 1 ; - 2 ) , v → = ( 1 ; 0 ; m ) . Tìm tất c giá trị của m để góc giữa u → , v → bằng 45 ° .
![]()
![]()
![]()
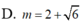
#2H3Y2-1~Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;3;2), B(2;-1;5) và C(3;2;-1). Gọi #$overrightarrow{AB}$,$overrightarrow{AC}$~ là tích có hướng của hai véc-tơ . Tìm tọa độ véc-tơ . A. (15;9;7) B. (9;3;-9). C. (3;-9;9)} D. (9;7;15)}
Đọc tiếp
#2H3Y2-1~Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;3;2), B(2;-1;5) và C(3;2;-1). Gọi ![]() #$\overrightarrow{AB}$,$\overrightarrow{AC}$~ là tích có hướng của hai véc-tơ
#$\overrightarrow{AB}$,$\overrightarrow{AC}$~ là tích có hướng của hai véc-tơ ![]() . Tìm tọa độ véc-tơ
. Tìm tọa độ véc-tơ ![]() .
.
A. ![]() = (15;9;7)
= (15;9;7)
B. ![]() = (9;3;-9).
= (9;3;-9).
C. ![]() = (3;-9;9)}
= (3;-9;9)}
D. ![]() = (9;7;15)}
= (9;7;15)}
Trong không gian tọa độ Oxyz, cho hai điểm A(1;-1;0) và B(1;2;-3). Tọa độ điểm M nằm trên trục Oz và cách đều hai điểm A, B là
A. M(0;0;-3)
B. M(0;0;-1)
C. M(0;0;-2)
D. M(0;0;2)
Trong không gian tọa độ Oxyz, cho điểm
M
(
a
;
b
;
c
)
. Tọa độ của véc-tơ
M
O
→
là
Đọc tiếp
Trong không gian tọa độ Oxyz, cho điểm M ( a ; b ; c ) . Tọa độ của véc-tơ M O → là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm A(1;-1;2) và có một véc tơ pháp tuyến
n
→
(
2
;
2
;
-
1
)
. Phương trình của (P) là: A. 2x + 2y - z - 7 0 B. 2x + 2y - z + 2 0 C. 2x + 2y - z - 6 0 D. 2x + 2y - z - 2 0
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm A(1;-1;2) và có một véc tơ pháp tuyến n → = ( 2 ; 2 ; - 1 ) . Phương trình của (P) là:
A. 2x + 2y - z - 7 = 0
B. 2x + 2y - z + 2 = 0
C. 2x + 2y - z - 6 = 0
D. 2x + 2y - z - 2 = 0