Đáp án D.
Phương pháp: Viết phương trình mặt phẳng (ABC) dạng đoạn chắn.
Cách giải: Phương trình mặt phẳng (ABC):
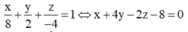
Đáp án D.
Phương pháp: Viết phương trình mặt phẳng (ABC) dạng đoạn chắn.
Cách giải: Phương trình mặt phẳng (ABC):
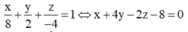
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a,b,c khác 0 Biết rằng mặt phẳng (ABC) đi qua điểm M 2 3 ; 4 3 ; 4 3 và tiếp xúc với mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 2 ) 2 = 1 Thể tích khối tứ diện OABC bằng
A. 4
B. 6
C. 9
D. 12
Trong không gian Oxyz, cho 2 điểm A(0;3;0), B(0;0;-4) và (P): x+2z=0. Gọi C thuộc trục Ox sao cho mặt phẳng (ABC) vuông góc với mặt phẳng (P). Tọa độ tâm mặt cầu ngoại tiếp tứ diện OABC là
A. ( 1 ; 3 2 ; - 2 )
B. ( - 1 ; - 3 2 ; 2 )
C. ( 1 2 ; 3 2 ; - 1 )
D. ( 1 ; 0 ; - 2 )
Trong không gian Oxyz, cho tam giác ABC vuông tại C, A B C ^ = 60 o , A B = 3 2 Đường thẳng AB có phương trình x - 3 1 = y - 4 1 = z + 8 - 4 đường thẳng AC nằm trên mặt phẳng α : x+z-1=0 Biết B là điểm có hoành độ dương, gọi (a;b;c) là tọa độ của điểm C, giá trị của a+b+c bằng
A. 3
B. 2
C. 4
D. 7
Trong không gian Oxyz, cho hai điểm M(1;2;3), A(2;4;4) và hai mặt phẳng (P):x+y-2z+1=0, (Q):x-2y-z+4=0. Đường thẳng ∆ đi qua điểm M, cắt hai mặt phẳng (P), (Q) lần lượt tại B và C(a;b;c) sao cho tam giác ABC cân tại A và nhận AM làm đường trung tuyến. Tính T=a+b+c.
A. T = 9
B. T = 3
C. T = 7
D. T = 5
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0
Tìm điểm N' là ảnh của N(0; 2; 4) quá phép đối xứng qua đường thẳng d.
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng: ∆ : x 1 = y - 1 1 = z - 2 - 1 và mặt phẳng ( P ) : x + 2 y + 2 z - 4 = 0 . Phương trình đường thẳng d nằm trong mặt phẳng (P) sao cho d cắt và vuông góc với đường thẳng Δ là
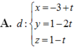
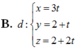
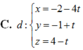
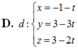
Trong không gian Oxyz, cho điểm A(1;2;-1), đường thẳng d: x - 1 2 = y + 1 1 = z - 2 - 1 và mặt phẳng (P):x+y+2z+1=0. Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là
A. (3;-2;-1)
B. (-3;8;-3)
C. (0;3;-2)
D. (6;-7;0)
Trong không gian với hệ tọa độ Oxyz cho đường thẳng ∆ : x 1 = y - 1 1 = z - 2 - 1 và mặt phẳng (P): x+2y+2z-4=0. Phương trình đường thẳng d nằm trong (P) sao cho d cắt và vuông góc với đường thẳng ∆ là
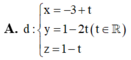
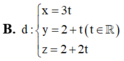
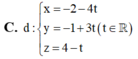
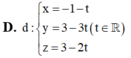
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a,b,c là các số thực thay đổi thỏa mãn 1 a - 1 b + 1 c = 1 . Biết rằng mặt cầu S : x - 2 2 + y - 1 2 + z - 3 2 = 25 cắt mặt phẳng (ABC) theo giao tuyến là một đường tròn có bán kính bằng 4. Giá trị của biểu thức a+b-c bằng
![]()
![]()
![]()
![]()