Chọn B
Nhận thấy AB=AC=AD=BC=DB=DC= 2 nên ABCD là tứ diện đều cạnh 2 .
Theo giả thiết giao tuyến của mặt cầu tiếp xúc 6 cạnh của tứ diện với (ACD) là đường tròn nội tiếp tam giác ACD.
Gọi r là bán kính hình tròn nội tiếp tam giác ACD
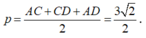
Khi đó diện tích tam giác đều ACD
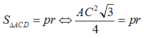
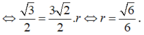
Diện tích thiết diện
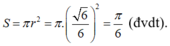
Cách 2:
Vì ABCD là tứ diện đều nên (ACD) cắt mặt cầu theo giao tuyến là đường tròn nội tiếp tam giác ACD . Suy ra tâm đường tròn này trùng với trọng tâm tam giác đều ACD và bán kính
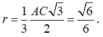
Diện tích thiết diện
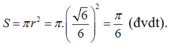
Đúng 0
Bình luận (0)

