Các câu hỏi tương tự
Trong không gian tọa độ Oxyz, cho mặt cầu (S):
(
x
-
2
)
2
+
y
2
+
(
z
+
1
)
2
9
và mặt phẳng (P): 2x-y-2z-30. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho mặt cầu (S): ( x - 2 ) 2 + y 2 + ( z + 1 ) 2 = 9 và mặt phẳng (P): 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính R của (C)
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(3;-2;6),B(0;1;0) và mặt cầu (S):
(
x
-
1
)
2
+
(
y
-
2
)
2
+
(
z
-
3
)
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai điểm A(3;-2;6),B(0;1;0) và mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 . Mặt phẳng (P): ax+by+cz-2=0 đi qua A và B và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T=a+b+c
A. T=3
B. T=5
C. T=2
D. T=4
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
(
P
)
:
x
−
y
+
2
z
+
1
0
và
(
Q
)
:
2
x
+
y
+
z
−
z
0.
Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q)...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( P ) : x − y + 2 z + 1 = 0 và ( Q ) : 2 x + y + z − z = 0. Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính r. Xác định r sao cho chỉ có duy nhất một mặt cầu (S) thỏa mãn điều kiện bài toán
A. r = 3 2 2 .
B. r = 10 2 .
C. r = 3 .
D. r = 14 2 .
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(3; 2;6), B(0;1;0) - và mặt cầu
(
S
)
:
x
-
1
2
+
y
-
2
2
+...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(3; 2;6), B(0;1;0) - và mặt cầu ( S ) : x - 1 2 + y - 2 2 + z - 3 2 = 25 . Mặt phẳng (P): ax+by+cz-2=0 đi qua A, B và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T =a+b+c.
A. T = 5
B. T = 3
C. T = 2
D. T = 4
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3;-2;6) ,B(0;1;0) và mặt cầu
(
S
)
:
x
-
1
2
+
y
-
2
2
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3;-2;6) ,B(0;1;0) và mặt cầu ( S ) : x - 1 2 + y - 2 2 + z - 3 2 = 25 . Mặt phẳng (P): ax+by+cz-2=0 đi qua A, B và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T=a+b+c.
A. T = 3
B. T = 5
C. T = 2
D. T = 4
Trong không gian Oxyz, cho điểm
A
(
0
;
1
;
2
)
, mặt phẳng
α
:
x
-
y
+
z
-
4
0
và mặt cầu
S
:
(
x
-
3...
Đọc tiếp
Trong không gian Oxyz, cho điểm A ( 0 ; 1 ; 2 ) , mặt phẳng α : x - y + z - 4 = 0 và mặt cầu S : ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 16 . Gọi (P) là mặt phẳng đi qua A, vuông góc với α và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
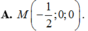
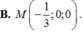
![]()
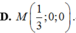
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
S
)
:
x
-
1
2
+
y
-
2
2
+
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S ) : x - 1 2 + y - 2 2 + z - 2 2 = 9 và mặt phẳng (P): 2x-y-2z+1=0. Biết (P) cắt (S) theo giao tuyến là đường tròn có bán kính r. Tính r.
A. r = 3
B. r = 2 2
C. r = 3
D. r = 2
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-40 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục xOx là:
A
.
M
-
1
2
;
0
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-4=0 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²=16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
A . M - 1 2 ; 0 ; 0
B . M - 1 3 ; 0 ; 0
C . M 1 ; 0 ; 0
D . M 1 3 ; 0 ; 0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - 2y + 2z - 2 0 và điểm I(-1;1;-1). Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5. A. B. C. D.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - 2y + 2z - 2 = 0 và điểm I(-1;1;-1). Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5.
A. ![]()
B. ![]()
C. ![]()
D. ![]()