Đáp án B
- Phương pháp:
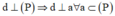
- Cách giải: Trong không gian cho đường thẳng Δ và điểm O. Qua O có vô số đường thẳng vuông góc Δ. Chúng nằm trong mặt phẳng qua O và vuông góc với Δ.
Đáp án B
- Phương pháp:
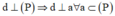
- Cách giải: Trong không gian cho đường thẳng Δ và điểm O. Qua O có vô số đường thẳng vuông góc Δ. Chúng nằm trong mặt phẳng qua O và vuông góc với Δ.
Trong không gian cho đường thẳng Δ và điểm O. Qua O có mấy đường thẳng vuông góc với Δ cho trước?
A. 1
B. 2
C. 3
D. Vô số.
Trong các mệnh đề sau đây mệnh đề nào là đúng?
a) Đường thẳng Δ là đường vuông góc chung của hai đường thẳng a và b nếu Δ ⊥a và Δ ⊥b.
b) Gọi (P) là mặt phẳng song song với cả hai đường thẳng a và b chéo nhau thì đường vuông góc chung của a và b luôn luôn vuông góc với (P).
c) Gọi Δ là đường vuông góc chung của hai đường thẳng chéo nhau a và b thì Δ là giao tuyến của hai mặt phẳng (a, Δ) và (b, Δ).
d) Cho hai đường thẳng chéo nhau a và b. Đường thẳng nào đi qua một điểm M trên a đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Đường vuông góc chung Δ của hai đường thẳng chéo nhau a và b nằm trong mặt phẳng chứa đường này và vuông góc với đường kia.
Cho hàm số 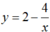 có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
A. y = x + 4.
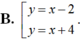
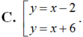
D. Không tồn tại.
Cho hai mặt phẳng (α) và (β) vuông góc với nhau và cắt nhau theo giao tuyến d. Chứng minh rằng nếu có một đường thẳng Δ nằm trong (α) và Δ vuông góc với d thì Δ vuông góc với (β)
1. Cho 2 Δđều OAB & ΔOA′B′. Gọi C, D lần lượt là trung điểm của AA', BB'. CM ΔOCD đều
2. Cho 2 Δ vuông cân OAB và OA'B' chung đỉnh O sao cho O nằm trên đoạn thẳng AB' và nằm ngoài đường thẳng A'B. Gọi G, G' lần lượt là trọng tâm ΔOAA′,ΔOBB′. CM ΔGOG′ vuông cân
Trong không gian nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a có vuông góc với c không?
Số phát biểu đúng
1. Trong không gian qua 1 điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy đồng quy
3. Nếu 2 mặt phẳng phân biệt lần lượt chứa 2 đường thẳng song song thì giao tuyến của chúng ( nếu có ) cũng song song với 2 đường thẳng đó hoặc trùng với một trong 2 đường thẳng đó
4. 2 đường thẳng phân biệt cùng song song với đường thẳng thứ 3 thì chúng song song với nhau
5. Nếu đường thẳng d không nằm trong mặt phẳng ( ) và d song song với đường thẳng d’ nằm trong ( ) thì d song song với ( )
6. Cho đường thẳng a song song với mặt phẳng . Nếu mặt phẳng chứa a và cắt theo giao tuyến b thì b song song với a
7. Nếu 2 mặt phẳng cùng song song với 1 đường thẳng thì giao tuyến của chúng ( nếu có ) cũng song song với đường thẳng đó
8. Cho 2 đường thẳng chéo nhau. Có vô số mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
A. 8
B. 7
C. 6
D. 5
Trong mặt phẳng với hệ tọa độ Oxy. Phép tịnh tiến theo vectơ biến đường thẳng Δ: x - y -1 = 0 thành đường thẳng Δ' có phương trình là
A.x - y - 1 = 0 .
B. x + y - 1 = 0 .
C. x - y - 2 = 0 .
D. x + y + 2 = 0 .
Xét các khẳng định sau đây xem khẳng định nào đúng, khẳng định nào sai?
a) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
b) Qua một đường thẳng, có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
c) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
d) Cho hai đường thẳng a và b. Nếu có mặt phẳng (α) không chứa cả a và b thì a và b chéo nhau.