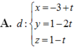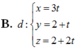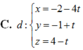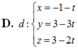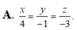Chọn A
Nhận thấy tam giác ABC đều có trọng tâm G (2;2;2), và OG ⊥ (ABC) nên hình chiếu của O lên (ABC) là điểm G
![]()
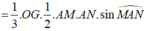
Vì OG và 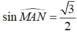 cố định nên thể tích
cố định nên thể tích ![]() nhỏ nhất khi và chỉ khi AM. AN nhỏ nhất.
nhỏ nhất khi và chỉ khi AM. AN nhỏ nhất.
Vì M, N, G thẳng hàng nên 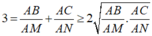 , suy ra
, suy ra ![]() . Đẳng thức xảy ra khi
. Đẳng thức xảy ra khi 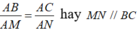 .
.
Khi đó mặt phẳng (P) đi qua O và nhận ![]() là một vectơ pháp tuyến, do đó (P): x+y-2z=0.
là một vectơ pháp tuyến, do đó (P): x+y-2z=0.