Chọn D.
Phương pháp: Tìm tập xác định.
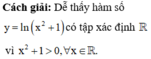
Chọn D.
Phương pháp: Tìm tập xác định.
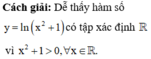
Tập xác định D của hàm số y = ln x + 2 là
A. D = [ 2 ; + ∞ )
B. D = [ e 2 ; + ∞ )
C. D = [ 1 e 2 ; + ∞ )
D. D = [ ln 2 ; + ∞ )
Tìm tập xác định của hàm số y = ln ( 1 - x + 1 ) là
A . [ - 1 ; 0 ]
B . ( - 1 ; + ∞ )
C . ( - 1 ; 0 )
D . ( - 1 ; 0 )
Tập xác định của hàm số y = l n ( x - 2 - x 2 - 3 x - 10 ) là
A. 5 ≤ x ≤ 14
B. 2 < x < 14
C. 2 ≤ x < 14
D. 5 ≤ x < 14
Cho hàm số y = x – ln(1 + ex). Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại x = 0
B. Tập xác định của hàm số là D = (0; +∞)
C. Hàm số đồng biến trên R
D. Hàm số đạt cực tiểu tại x = 1
Đạo hàm của hàm số y = x + 2 x - 1 ln ( x + 2 ) là
A. y ' = 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
B. y ' = x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
C. y ' = 2 x log ( 2 x - 1 ) + 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
D. y ' = - 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
Cho hàm số y = f(x) = ln(x+1). Mệnh đề nào sau đây là đúng?
A. Đồ thị của hàm số y = f'(x) cắt trục hoành tại 1 điểm
B. Phương trình f'(x) = 0 có nghiệm x = 1
C. Đồ thị của hàm số y = f'(x) không cắt trục hoành
D. Phương trình f'(x) = 0 có nghiệm x = -1
Hàm số y = ln ( x + 2 ) + 3 x + 2 đồng biến trên khoảng nào sau đây?
A. - ∞ ; 1
B. 1 ; + ∞
C. 1 2 ; 1
D. - 1 2 ; + ∞
Cho hàm số y = ln x. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng 0 ; + ∞
B. Hàm số có tập giá trị là - ∞ ; + ∞
C. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng
D. Hàm số có tập giá trị là 0 ; + ∞
Cho hàm số y = ln x. Khẳng định nào sau đây là khẳng định sai?
A. Hàm số đồng biến trên khoảng 0 ; + ∞
B. Hàm số có tập giá trị là - ∞ ; + ∞
C. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng
D. Hàm số có tập giá trị là 0 ; + ∞
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f(-1) = 1, f - 1 e = 2 . Bất phương trình f(x) < ln(-x) + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
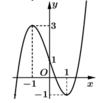
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3