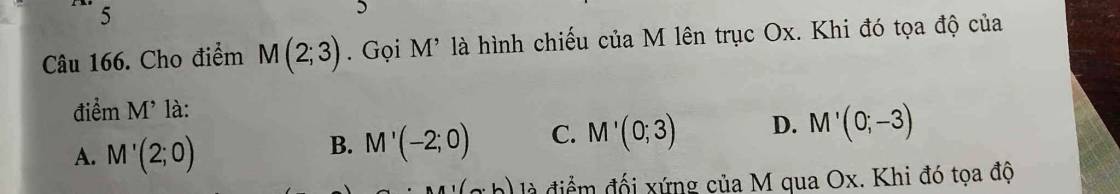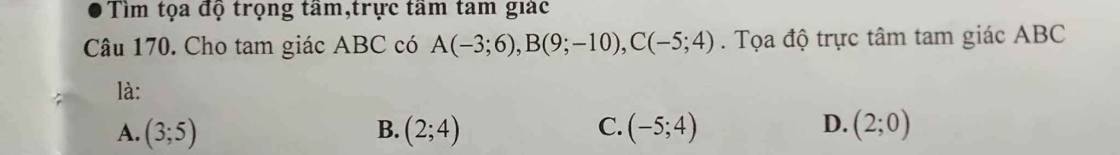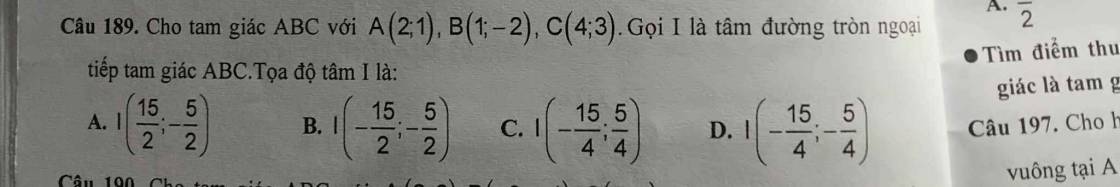Câu 170:
Gọi $H(a,b)$ là tọa độ trực tâm của tam giác $ABC$
Có:
$AH\perp BC$
$\Leftrightarrow \overrightarrow{AH}.\overrightarrow{BC}=0$
$\Leftrightarrow (a+3, b-6).(-14,14)=0$
$\Leftrightarrow -14(a+3)+14(b-6)=0$
$\Leftrightarrow -a-3+b-6=0$
$\Leftrightarrow -a+b=9(1)$
$BH\perp AC$
$\Leftrightarrow \overrightarrow{BH}.\overrightarrow{AC}=0$
$\Leftrightarrow (a-9, b+10).(-2, -2)=0$
$\Leftrightarrow -2(a-9)-2(b+10)=0$
$\Leftrightarrow a-9+b+10=0$
$\Leftrightarrow a+b=-1(2)$
Từ $(1); (2)\Rightarrow a=-5; b=4$
Đáp án C.
Câu 189:
Gọi $I(a,b)$ là tâm đường tròn ngoại tiếp tam giác $ABC$.
$M(\frac{3}{2}, \frac{-1}{2}), N(\frac{5}{2}, \frac{1}{2})$ lần lượt là trung điểm của $AB, BC$
Có:
$IM\perp AB$
$\Leftrightarrow \overrightarrow{MI}.\overrightarrow{AB}=0$
$\Leftrightarrow (a-\frac{3}{2}, b+\frac{1}{2}).(-1, -3)=0$
$\Leftrightarrow -(a-\frac{3}{2})-3(b+\frac{1}{2})=0$
$\Leftrightarrow a-\frac{3}{2}+3b+\frac{3}{2}=0$
$\Leftrightarrow a+3b=0(1)$
Lại có:
$IN\perp BC$
$\Leftrightarrow \overrightarrow{NI}.\overrightarrow{BC}=0$
$\Leftrightarrow (a-\frac{5}{2}, b-\frac{1}{2})(3,5)=0$
$\Leftrightarrow 3(a-\frac{5}{2})+5(b-\frac{1}{2})=0$
$\Leftrightarrow 3a+5b=10(2)$
Từ $(1); (2)\Rightarrow a=\frac{15}{2}; b=\frac{-5}{2}$
Đáp án A.
Câu 166:
$M'\in Ox$ nên $y_M=0$
$MM'\perp Ox$
$\Leftrightarrow (x_M'-x_M, y_M'-y_M)\perp (1,0)
$\Leftrightarrow (x_M'-2).1+(y_M'-3).0=0$
$\Leftrightarrow x_M'=2$
Đáp án A