là góc tạo bởi tiếp tuyến CT và dây CD
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao chosđ
A
C
⏜
sđ
C
D
⏜
sđ
D
B
⏜
60
o
Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:...
Đọc tiếp
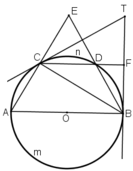
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho
sđ A C ⏜ = sđ C D ⏜ = sđ D B ⏜ = 60 o
Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
A E B ^ = B T C ^
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho
sd
AC
^
sd
CD
→
sd
DB
^
60
°
Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:a).
AEB
^
BTC
^
b) CD là tia phân giác của góc BCT
Đọc tiếp
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho
sd AC ^ = sd CD → = sd DB ^ = 60 °
Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
a). AEB ^ = BTC ^
b) CD là tia phân giác của góc BCT
Trên đường tròn tâm O đường kính AB=2R , lấy điểm C sao cho sđ cung BC=60° . Hai tiếp tuyến với đường tròn vẽ từ B và C cắt nhau tại D . a) Tính sđ góc BOC và sđ cung nhỏ AC . b) chứng minh tứ giác OBDC nội tiếp . c) Tia AC cắt tia BD tại E . Chứng minh D là trung điểm của BE . d) Biết R=15cm . Tính diện tích hình quạt giới hạn bởi cung nhỏ AC( biết π=3,14)
Trên đường tròn lấy liên tiếp 3 cung AC ,CD,DB sao cho số đo của cung AC bằng số đo của cung góc AC = số đo của cung góc CD =60° hai đường thẳng AC và BD cắt nhau tại E hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T chứ minh rằng a, góc AEB = góc BTC. b, CD là tia phân giác của góc BTC M.n giúp em với ạ
Bài 4 Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Hai đường thẳng DE và BC cắt nhau tại F. Chứng minh rằng:a) Tứ giác BCDE nội tiếp.b)góc AFE ACE.Bài 5. Cho nứa đường tròn đường kính AB. Lấy hai điểm C và D trên nửa đường tròn sao cho cung AC cung CD cung DB. Các tiếp tuyến vẽ từ B và C của nửa đường tròn cắt nhau tại I.Hai tia AC và BD cắt nhau tại K. Chứng minh rằng:a) Các tam giác KAB và IBC là những tam giác đêu.b) Tứ giác KIBC nội tiếp.Bài 6. C...
Đọc tiếp
Bài 4 Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Hai đường thẳng DE và BC cắt nhau tại F. Chứng minh rằng:
a) Tứ giác BCDE nội tiếp.
b)góc AFE= ACE.
Bài 5. Cho nứa đường tròn đường kính AB. Lấy hai điểm C và D trên nửa đường tròn sao cho cung AC= cung CD= cung DB. Các tiếp tuyến vẽ từ B và C của nửa đường tròn cắt nhau tại I.Hai tia AC và BD cắt nhau tại K. Chứng minh rằng:
a) Các tam giác KAB và IBC là những tam giác đêu.
b) Tứ giác KIBC nội tiếp.
Bài 6. Cho nửa đường tròn (0) đường kính AB và tia tiếp tuyến Bx của nửa đường tròn. Trên tia Bx lấy hai điểm C và D (C nằm giữa B và D). Các tia AC và BD lần lượt cắt đường tròn tại E và F. Hai dây AE và BF cắt nhau tại M. Hai tia AF và BE cắt nhau tại N. Chứng minh rằng:
a) Tứ giác FNEM nội tiêp.
b) Tứ giác CDFE nội tiếp.
Bài 7. Cho tam giác ABC. Hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC.
a) Chứng minh rằng tứ giác ABDC nội tiếp được đường tròn. Xác định tâm 0 của đường tròn đó
b) Đường thẳng DH cắt đường tròn (0) tại điểm thứ hai là I. Chứng minh rằng năm điểm A, I, F, H, E cùng nằm trên một đường tròn
Các bạn giải giúp mình các bài này nhé, mình cảm ơn nhiều lắm
Cho nửa đường tròn (O) đường kính AB. Trên nửa đường tròn đó lấy hai điểm C,D sao cho cung AC = cung CD = cung DB. Các tiếp tuyến của nửa đường tròn vẽ từ B và C cắt nhau tại I. Hai tia AC và BD cắt nhau tại K.Cm:
a) Tứ giác ACDB là hình thang cân
b) Các tam giác KAB và IBC là tam giác đều
c) Tứ giác KIBC nột tiếp.
Giải giúp mình với!!! Help meee
Cho tam giác ABC nội tiếp đường tròn (O) đường kính BC(AB<AC, góc AOB>60 độ), D là một điểm thuộc cung nhỏ AB sao cho DA=DB. Đường trung trực của đoạn OA cắt đường tròn (O) tại E và F(F thuộc cung nhỏ AC)
a)CMR sđ cung FC=2 sđ cung DE
b)Đường thẳng qua O song song với DA cắt AC tại J. CMR EJ là phân giác của góc CEF
Cho đường tròn (O;R) có đường kính AB, lấy điểm C trên đường tròn sao cho góc AOC là góc tù, vẽ OH vuông góc với AC tại H tiếp tuyến tại A của đường tròn cắt OH tại D. DB cắt đường tròn tại E. Gọi F là ttrung điểm của BEa, Cm DC là tiếp tuyến của đường tròn và điểm A, D, C, F, O cùng thuộc 1 đường trònb, Cm DA2 DE.DB và góc EHD góc EBOc. CHứng minh HC là tia phân giác góc EHBd. Tiếp tuyến tại B của (O) cắt tia AC tại K. Chứng minh ba điểm O, F,K thẳng hàng .AI GIÚP EM VỚI Ạ
Đọc tiếp
Cho đường tròn (O;R) có đường kính AB, lấy điểm C trên đường tròn sao cho góc AOC là góc tù, vẽ OH vuông góc với AC tại H tiếp tuyến tại A của đường tròn cắt OH tại D. DB cắt đường tròn tại E. Gọi F là ttrung điểm của BE
a, Cm DC là tiếp tuyến của đường tròn và điểm A, D, C, F, O cùng thuộc 1 đường tròn
b, Cm DA2 = DE.DB và góc EHD = góc EBO
c. CHứng minh HC là tia phân giác góc EHB
d. Tiếp tuyến tại B của (O) cắt tia AC tại K. Chứng minh ba điểm O, F,K thẳng hàng .
AI GIÚP EM VỚI Ạ
Cho nữa đường tròn đường kính AB trên nữa đường tròn đó lấy 2 điểm C và D sao cho cung AC, CD, DB bang nhau, các tiếp tuyến kẻ từ C và B của đường tròn cắt nhau tại I, AC cắt DB tại K. Chứng minh rằng:
a) Tam giácOAC, OCD, OBD là 3 tam giác đều.
b) Tứ giác KIBC là tứ giác nội tiếp.
c) AIBK là hình thang vuông.
d) tính diện tích hình thang AIBK theo a=OA