a) Trên hình bên. Cung có số đo 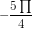
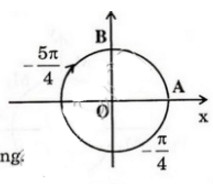
b) Nhận xét rằng 1350 – ( -2250 ) = 3600 . Như vậy cung 1350 và cung -2250 có chung điểm ngọn. Mà cung 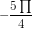 cũng là cung -2250 . Vậy cung 1350 cũng chính là cung theo chiều dương
cũng là cung -2250 . Vậy cung 1350 cũng chính là cung theo chiều dương
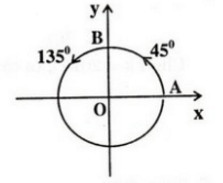
c) 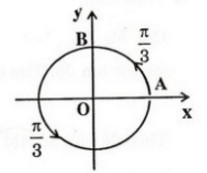
d) 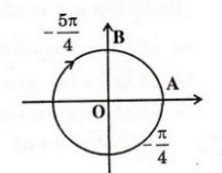
a) Trên hình bên. Cung có số đo 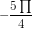

b) Nhận xét rằng 1350 – ( -2250 ) = 3600 . Như vậy cung 1350 và cung -2250 có chung điểm ngọn. Mà cung 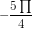 cũng là cung -2250 . Vậy cung 1350 cũng chính là cung theo chiều dương
cũng là cung -2250 . Vậy cung 1350 cũng chính là cung theo chiều dương

c) 
d) 
Một đường tròn có bán kính 25 cm. Tìm độ dài của các cung trên đường tròn đó có số đo :
a) \(\dfrac{3\pi}{7}\)
b) \(49^0\)
c) \(\dfrac{4}{3}\)
Trên đường tròn lượng giác gốc A, xác định các điểm M khác nhau, biết rằng cung AM có số đo tương ứng là (trong đó k là một số nguyên tùy ý)
a) \(k\pi\)
b) \(k\dfrac{\pi}{2}\)
c) \(k\dfrac{\pi}{3}\)
Xác định điểm cuối của các cung lượng giác
a) \(\alpha=\dfrac{-2\pi}{3}\)
b) \(\alpha=k.2\pi\)
c) \(\alpha=\pi+k.2\pi\)
d) \(\alpha=\dfrac{\pi}{3}+k.\pi\)
e) \(\alpha=\dfrac{\pi}{4}+\dfrac{k.\pi}{2}\)
Trên đường tròn lượng giác gốc A cho các cung có số đo:
I. \(\dfrac{\pi}{4}\) II. \(-\dfrac{7\pi}{4}\) III. \(\dfrac{13\pi}{4}\) IV. \(-\dfrac{71\pi}{4}\)
Một đường tròn có bán kính 20cm. Tìm độ dài của các cung trên đường tròn đó có số đo :
a) \(\dfrac{\pi}{15}\)
b) \(1,5\)
c) \(37^o\)
Trên đường tròn lượng giác cho điểm M xác định bởi sđ AM = \(\alpha\left(0< \alpha< \dfrac{\pi}{2}\right)\). Gọi \(M_1;M_2;M_3\) lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc tọa độ. Tìm số đo của các cung \(AM_1;AM_2;AM_3\)
Đổi số đo của các cung sau đây ra độ, phút, giây :
a) \(\dfrac{\pi}{18}\)
b) \(\dfrac{3\pi}{16}\)
c) \(-2\)
d) \(\dfrac{3}{4}\)
Tìm số điểm biểu diễn cung có số đo \(x=\frac{\pi}{4}+\frac{k\pi}{3}\)trên khoảng \(\left(\frac{-2\pi}{3};\frac{5\pi}{6}\right)\)
Tìm số \(x\left(0\le x< 2\pi\right)\) và số nguyên k sao cho \(a=x+k2\pi\) trong các trường hợp
a) \(a=12,4\pi\)
b) \(a=-\dfrac{9}{5}\pi\)
c) \(a=\dfrac{13}{4}\pi\)