Question

Trên các cạnh AB, BC, CD và DA của hình vuông ABCD ta lấy lần lượt các điểm E, F, G, H sao cho AE = BF = CG = DH. Các đường chéo AC và BD cắt nhau ở O.

a) Chứng minh rằng ba điểm F, O, H thẳng hàng.

b) Chứng minh rằng điểm O cách đều bốn điểm E, F, G, H.

vẽ hình nữa ạ!

Answer 1

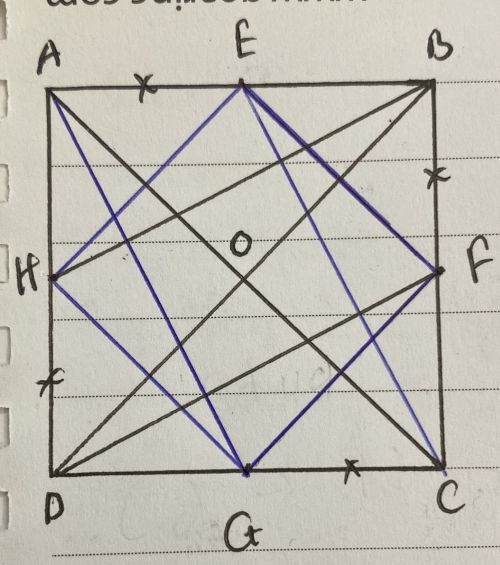
a) Xét tứ giác BFDH có:

BF = DH (giả thiết).

BF // DH (do ABCD hình vuông).

=> BFDH hình bình hành.

Theo GT: O là giao điểm của AC và BD.

Do đó O thuộc FH (vì BD và HF giao điểm của hình bình hành BFDH)

Vậy ba điểm F, O, H thẳng hàng.

b) Theo cmt câu a F, O, H thẳng hàng.

O trung điểm hai đường chéo AC và BD trong hình vuông ABCD.

=> H, F lần lượt là trung điểm của AD và BC.

Xét ΔBEF=ΔCFG có:

+ Góc EBF = Góc FCG

+ BF = CG

=> ΔBEF=ΔCFG (cgv – cgv) nên EF = FG.

Chứng minh tương tự FG = GH, GH = HE

=> EF = FG = GH = HE.

=> EFGH là hình vuông.

Xét tứ giác AECG có:

AE = CG (giả thiết).

AE // CG (do ABCD hình vuông).

=> AECG hình bình hành.

Theo GT: O là giao điểm của AC và BD.

Do đó O thuộc EG (vì BD và EG giao điểm của hình bình hành AECG)

Xét Hình vuông EFGH có:

O thuộc HF

O thuộc EG

=> O cách đều bốn điểm E, F, G, H.