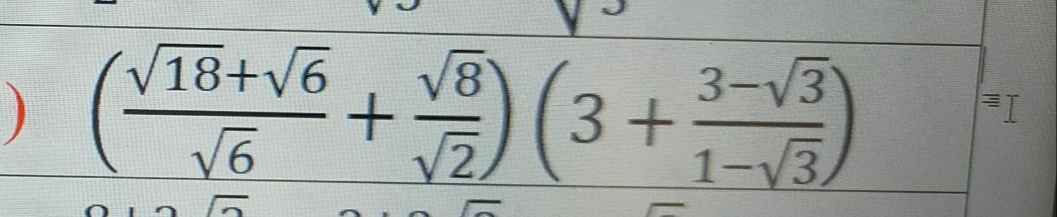\(\left(\dfrac{\sqrt{2\cdot3^2}+\sqrt{2\cdot3}}{\sqrt{2\cdot3}}+\dfrac{\sqrt{2\cdot2^2}}{\sqrt{2}}\right)\left(3+\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\right)\)
\(=\left(\dfrac{3\sqrt{2}+\sqrt{6}}{\sqrt{6}}+\dfrac{2\sqrt{2}}{\sqrt{2}}\right)\left(3-\dfrac{\sqrt{3}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right)\)
\(=\left(\dfrac{3\sqrt{2}+\sqrt{6}}{\sqrt{6}}+2\right)\left(3-\sqrt{3}\right)\)
\(=\left(\dfrac{3\sqrt{2}+\sqrt{6}+2\sqrt{6}}{\sqrt{6}}\right)\left(3-\sqrt{3}\right)\)
\(=\left(\dfrac{3\sqrt{2}+3\sqrt{6}}{\sqrt{6}}\right)\left(3-\sqrt{3}\right)\)
\(=\dfrac{\left(3\sqrt{2}+3\sqrt{6}\right)\left(3-\sqrt{3}\right)}{\sqrt{6}}\)
\(=\dfrac{9\sqrt{2}-3\sqrt{6}+9\sqrt{6}-3\sqrt{18}}{\sqrt{6}}\)
\(=\dfrac{9\sqrt{2}+6\sqrt{6}-3\sqrt{2\cdot3^2}}{\sqrt{6}}\)
\(=\dfrac{9\sqrt{2}+6\sqrt{6}-9\sqrt{2}}{\sqrt{6}}\)
\(=\dfrac{6\sqrt{6}}{\sqrt{6}}\)
\(=6\)