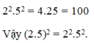Các câu hỏi tương tự
Câu 1: Chứng minh:
\(31.82+125.48+21.43=125.67=1500\)
Câu 2: So sánh:
1,\(\sqrt{51}-\sqrt{5}v\text{à}\sqrt{20}-\sqrt{6}\)
2,\(\sqrt{2}+\sqrt{8}v\text{à}\sqrt{3}+3\)
3,\(\sqrt{37}-\sqrt{14}v\text{à}6-\sqrt{15}\)
4,\(\sqrt{5}+\sqrt{10}v\text{à}5,3\)
So sánh :
\(a,2^{30}v\text{à}3^{20}\)
\(b,5^{300}v\text{à}3^{500}\)
\(c,2^{24}v\text{à}3^{16}\)
\(d,\left(0,3\right)^{40}v\text{à}\left(0,1\right)^{20}\)
So sánh:
\(\left(-\frac{1}{5}\right)^{255}v\text{à}\left(-\frac{1}{2}\right)^{579}\)
Bài 1: So sánh các số sau:(so sánh bằng cách nhanh nhất)
a) -17 và 23 b)-1 và 2 c) 2 và 5 d)267 và -1347
36 -48 3 5 7 4 -268 1343
Bài 2: Tính bằng 2 cách:
5 -(1 3-0,4)
2 7
So sánh
\(a,2^{30}+3^{30}+4^{30}v\text{à}3^{20}+6^{20}+8^{20}\)
\(b,2^{30}+3^{30}+4^{30}v\text{à}3.24^{10}\)
\(c,2^0+2^1+2^2+...+2^{50}v\text{à}2^{51}\)
1. so sánh
\(2^{27}v\text{à}3^{18}\)
\(3^{21}v\text{à}2^{31}\)
So sánh:
a)\(2^{24}v\text{à}3^{16}\)
b)\(2^{300}v\text{à}3^{200}\)
c)\(71^5v\text{à}7^{20}\)
CHO A = (1/22 - 1 ).( 1/32 - 1 ).(1/ 42 - 1 ).........(1/20132 - 1 ).(1/20142 -1) VÀ B = -1/2 . SO SÁNH A VÀ B
so sánh \(\frac{1}{101^2}+\frac{1}{102^2}+...+\frac{1}{205^2}v\text{à}\frac{1}{2^2\cdot3\cdot5^2\cdot7}\)
NN
20 tháng 12 2022 lúc 15:29
1 so sánh \(\dfrac{1}{2^{300}}\) và \(\dfrac{1}{300^{200}}\)
\(\dfrac{1}{5^{199}}\) và\(\dfrac{1}{3^{300}}\)
2 so sánh
5\(^{20}\)và 3\(^{34}\)
(-5)\(^{39}\)và -2\(^{91}\)