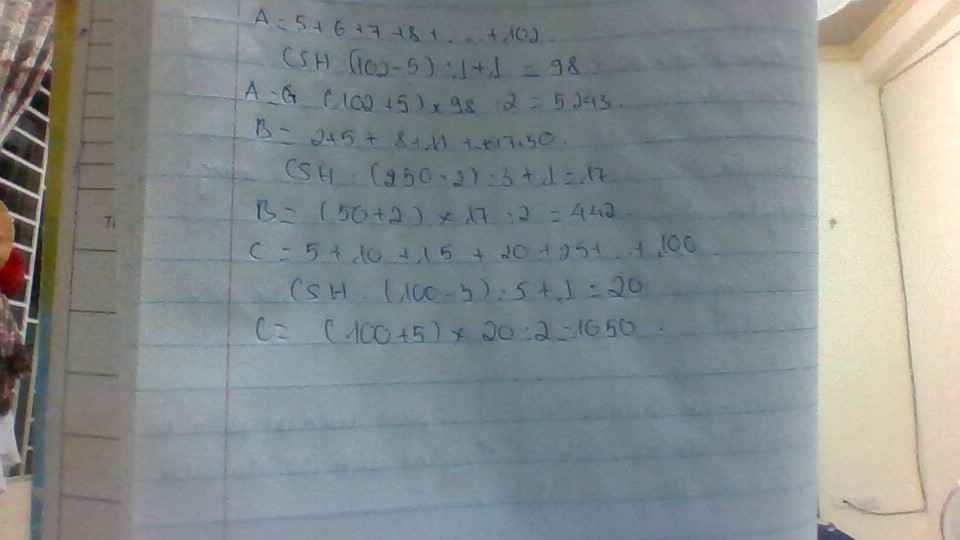Lời giải:
Số số hạng của $A$: $\frac{102-5}{1}+1=98$
$A=\frac{(102+5).98}{2}=5243$
Số số hạng của $B$: $\frac{50-2}{3}+1=17$
$B=\frac{(50+2).17}{2}=442$
Số số hạng của $C$: $\frac{100-5}{5}+1=20$
$C=\frac{(100+5).20}{2}=1050$
Đúng 1
Bình luận (0)
\(A=5+6+7+8+...+102=\left(102+5\right).\left(\dfrac{102-5}{1}+1\right)=10486\)
\(B=2+5+8+11+...+47+50=\left(50+2\right).\left(\dfrac{50-2}{3}+1\right)=884\)
\(C=5+10+15+20+25+...+100=\left(100+5\right).\left(\dfrac{100-5}{5}+1\right)=2100\)
Đúng 0
Bình luận (1)