Đáp án B
Điều kiện: tan x > 0
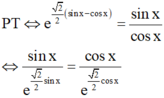
Xét hàm số y = f t = t e 2 2 t t ∈ - 1 ; 1
Khi đó f ' t = e 2 2 1 - t 2 2 e 2 t > 0 ∀ t ∈ - 1 ; 1
do đó hàm số f(t) đồng biến trên [–1;1]
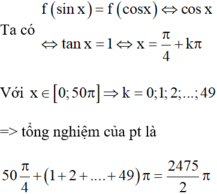
Đáp án B
Điều kiện: tan x > 0
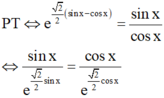
Xét hàm số y = f t = t e 2 2 t t ∈ - 1 ; 1
Khi đó f ' t = e 2 2 1 - t 2 2 e 2 t > 0 ∀ t ∈ - 1 ; 1
do đó hàm số f(t) đồng biến trên [–1;1]
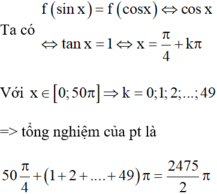
Tính tổng T tất cả các nghiệm của phương trình 2017 sin 2 x - 2017 cos 2 x = cos 2 x trên đoạn 0 ; π
A. x = π
B. x = π 4
C. x = π 2
D. x = 3 π 4
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình bên. Phương trình f( 2 sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn - π ; π khi và chỉ khi
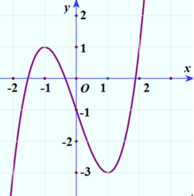
A. m ∈ - 3 ; 1
B. m ∈ - 3 ; 1
C. m ∈ [ - 3 ; 1 )
D. m ∈ ( - 3 ; 1 ]
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = -π/4 và x = π/4 bằng:
A. π; B. -π;
C. ln2; D. 0
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = - π /4 và x = π /4 bằng:
A. π ; B. - π ;
C. ln2; D. 0
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π /2 bằng:
A. 1; B. 2/7;
C. 2 π ; D. 2 π /3.
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) = m có nghiệm thuộc khoảng 0 ; π là

![]()
![]()
![]()
![]()
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(sin x) = 2sin x +m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng:
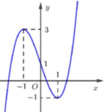
A. -10
B. -8
C. -6
D. -5
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
Tìm tổng các giá trị nguyên của tham số m để phương trình 4 sin x + 2 1 + sin x = m có tổng các nghiệm trong khoảng 0 ; π bằng π
A. 22
B. 25
C. 30
D. 33
∫ - π 2 π 2 sin 2 x . sinx 2 + cos 3 x d x bằng:
A. 2 B. 2 π
C. π D. - π