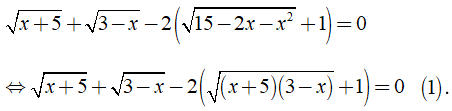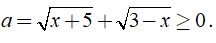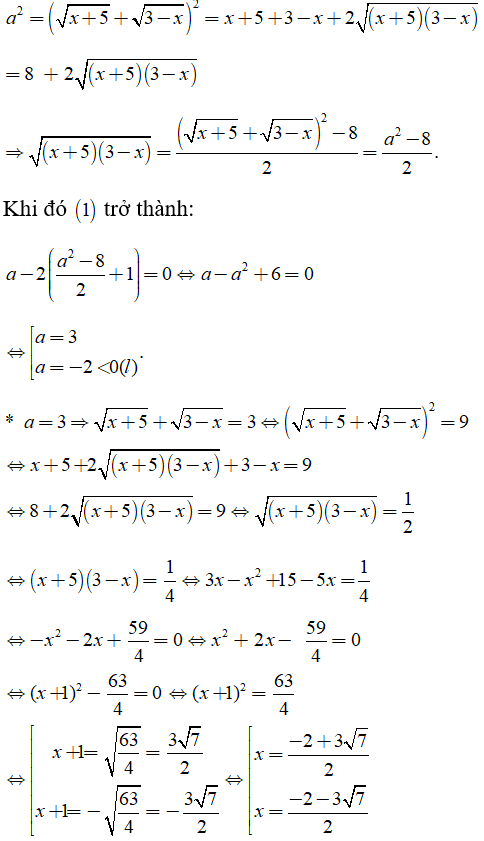ĐK: \(x\in\left[-5;3\right]\\ PT< =>\sqrt{x+5}+\sqrt{3-x}-2\left(\sqrt{\left(x+5\right)\left(3-x\right)}+1\right)=0\left(1\right)\)
Đặt \(a=\sqrt{x+5}+\sqrt{3-x}\left(a\ge0\right)\)
Ta có: \(a^2=\left(\sqrt{x+5}+\sqrt{3-x}\right)^2=x+5+3-x+2\sqrt{\left(x+5\right)\left(3-x\right)}\\ =8+2\sqrt{\left(x+5\right)\left(3-x\right)}\\ =>\sqrt{\left(x+5\right)\left(3-x\right)}=\dfrac{\left(\sqrt{x+5}+\sqrt{3-x}\right)^2-8}{2}\)
=\(\dfrac{a^2-8}{2}\)
\(PT\left(1\right)< =>a-2\left(\dfrac{a^2-8}{2}+1\right)=0\\ < =>a-a^2+6=0\)
Giải PT bậc 2 ta được: \(\left[{}\begin{matrix}a=3\left(Nhận\right)\\a=-2\left(loại\right)\end{matrix}\right.\)
=> \(\sqrt{x+5}+\sqrt{3-x}=3\)
\(< =>\left(\sqrt{x+5}+\sqrt{3-x}\right)^2=9\)
\(< =>8+2\sqrt{\left(x+5\right)\left(3-x\right)}=9\\ < =>\sqrt{\left(x+5\right)\left(3-x\right)}=\dfrac{1}{2}\\ < =>\left(x+5\right)\left(3-x\right)=\dfrac{1}{4}\\ < =>3x-x^2+15-5x=\dfrac{1}{4}\\ < =>x^2+2x-\dfrac{59}{4}=0\)
Giải PT bậc 2 ta được :\(\left[{}\begin{matrix}x_1=\dfrac{-2+3\sqrt{7}}{2}\\x_2=\dfrac{-2-3\sqrt{7}}{2}\end{matrix}\right.\)
Kết luận nghiệm của pt là......
Tham khảo ạ:
Điều kiện x ∈ [-5; 3]
Ta có:
Đặt
Khi đó