Ta có:
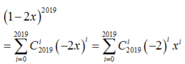
Tổng các hệ số trong khai triển
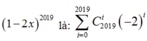
Cho
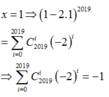
Vậy, tổng các hệ số trong khai triển 1 - 2 x 2019 là -1.
Chọn: A
Ta có:
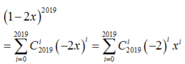
Tổng các hệ số trong khai triển
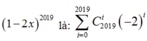
Cho
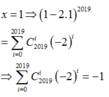
Vậy, tổng các hệ số trong khai triển 1 - 2 x 2019 là -1.
Chọn: A
Trong khai triển Newton của biểu thức ( 2 x - 1 ) 2019 , số hạng chứa x 18 là
A. - 2 18 . C 2019 18
B. - 2 18 . C 2019 18 . x 18
C. 2 18 . C 2019 18
D. 2 18 . C 2019 18 . x 18
Trong khai triển nhị thức Niutơn của a + 2 n + 6 có tất cả 2019 số hạng . Khi đó giá trị n bằng
A. 2012
B. 2013
C. 2018
D. 2019
Tổng các hệ số nhị thức Niu – tơn trong khai triển ( 1 + x ) 3 n bằng 64. Số hạng không chứa x trong khai triển ( 2 n x + 1 2 n x 2 ) 3 n là
A. 360
B. 210
C. 250
D. 240
Xét các khẳng định sau
i) Nếu a > 2019 thì a x > 2019 x ∀ x ∈ ℝ
ii) Nếu a > 2019 thì b a > b 2019 ∀ b > 0
iii) Nếu a > 2019 thì log b a > log b 2019 ∀ n > 0 ; b ≢ 0
Số khẳng định đúng trong các khẳng định trên là:
A. 3
B. 1
C. 2
D. 0
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d thỏa mãn a,b,c,dÎR; a > 0 và d > 2019 8 a + 4 b + 2 x + d - 2019 < 0 . Số cực trị của hàm số y = | f ( x ) - 2019 | bằng
A. 3
B. 2
C. 1
D. 5
Tính tổng các hệ số trong khai triển 1 − 2 x 2018 .
A. - 1
B. -2018
C. 2018
D. 1
Cho hàm số f(x) = ( x - 1 )( x - 2 )( x - 3 )...( x - 2019 ). Tính f '(1)
A. 0
B. 1
C. 2018!
D. 2019!
Tổng các hệ số nhị thức Niu – tơn trong khai triển ( 1 + x ) 3 n bằng 64. Số hạng không chứa x trong khai triển ( 2 n x + 1 2 n x 2 ) 3 n là
A. 360
B. 210
C. 250
D. 240
Cho khai triển 1 + x n 1 + 3 x = a 0 + a 1 x + a 2 x + . . . + a n + 1 x n + 1 . Tìm hệ số lớn nhất trong khai triển trên biết rằng tổng các hệ số của khai triển đó bằng 2 20 .
A. 277134
B. 189618
C. 48620
D. 179894