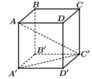
Giả sử khối lập phương có cạnh bằng x(x > 0)
Suy ra A'C' = x 2
Xét tam giác AA'C' vuông tại A' ta có
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Giả sử khối lập phương có cạnh bằng x(x > 0)
Suy ra A'C' = x 2
Xét tam giác AA'C' vuông tại A' ta có
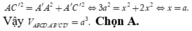
Tính thể tích V của khối lập phương ABCD.A' B' C' D' , biết AC'=a 3
A. V= 3 3 a 3
B. V= 27 a 3
C. V= a 3
D. V= 3 a 3
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0;1;0), B(2;2;2), C(-2;3;1) và đường thẳng d : x - 1 2 = y + 2 - 1 = z - 3 2 . Tìm điểm M thuộc d để thể tích V của tứ diện MABC bằng 3.
A. M 1 - 15 2 ; 9 4 ; - 11 2 , M 2 - 3 2 ; - 3 4 ; 1 2
B. M 1 - 3 5 ; - 3 4 ; 1 2 , M 2 - 15 2 ; 9 4 ; 11 2
C. M 1 3 2 ; - 3 4 ; 1 2 , M 2 15 2 ; 9 4 ; 11 2
D. M 1 3 5 ; - 3 4 ; 1 2 , M 2 15 2 ; 9 4 ; 11 2
Trong không gian Oxyz, cho hình bình hành ABCD với A(1; 2; 3), B(5; 0; -1), C(4; 3; 6) và D(a;b;c) Giá trị của a+b+c bằng
A. 3
B. 11
C. 15
D. 5
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x a + y 2 a + z 3 a = 1 (a>0) cắt ba trục Ox, Oy, Oz lần lượt tại 3 điểm A, B, C. Tính diện tích V của khối tứ diện OABC
A. V= a 3
B. V=3 a 3
C. V=2 a 3
D. V=4 a 3
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có A B = a , A A ' = 2 a . Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là 9 π 2 a 3 . Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′.
A. 4 a 3
B. 4 a 3 3
C. 2 a 3
D. 2 a 3 3
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Tính thể tích V của khối chóp D ' . A B C D .
A. V = a 3 4
B. V = a 3 6
C. V = a 3 3
D. V = a 3
Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là hình vuông cạnh bằng 4cm, đường chéo AB′ của mặt bên (ABB′A′) có độ dài bằng 5cm. Tính thể tích V của khối lăng trụ ABCD.A′B′C′D′.
A. 48 cm 3
B. 24 cm 3
C. 16 cm 3
D. 32 cm 3
Cho hình chóp S.ABCD có cạnh bên S A = a 0 < a < 3 và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD.
A. V = a 3 - a 2 3
B. đáp án khác
C. 2 2
D. 2
Cho khối chóp tam giác đều S.ABCD có cạnh đáy bằng a , S A = 3 . Tính thể tích V của khối chóp S.ABCD
A. V = 35 a 3 24
B. V = 3 a 3 6
C. V = 2 a 3 6
D. V = 2 a 3 2