Đáp án A
Ta có| V = π ∫ a b f 2 x d x .
Đáp án A
Ta có| V = π ∫ a b f 2 x d x .
Cho hàm số y=f(x) liên tục trên đoạn a ; b và f(x)>0 ∀ x ∈ a ; b Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b (a<b). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
A. ∫ a b f ( x 2 ) d x
B. π ∫ a b f ( x 2 ) d x
C. π ∫ a b [ f ( x ) ] 2 d x
D. ∫ a b [ f ( x ) ] 2 d x
Cho hàm số y = f ( x ) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f ( x ), trục hoành và hai đường thẳng x = a, x = b ( a > b ). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
A. V = π ∫ a b f 2 x dx
B. V = 2 π ∫ a b f 2 x dx
C. V = π 2 ∫ a b f 2 x dx
D. V = π 2 ∫ a b f x dx
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x) trục hoành và hai đường thẳng x=a, x=b (a<b). Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
A. V = π ∫ a b f 2 x dx
B. V = 2 π ∫ a b f 2 x dx
C. V = π 2 ∫ a b f 2 x dx
D. V = π 2 ∫ a b f x dx
Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) trục hoành và hai đường thẳng x = a , x = b a < b . Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
A. V = π ∫ a b f 2 x d x
B. V = π 2 ∫ a b f 2 x d x
C. V = π 2 ∫ a b f x d x
D. V = 2 π ∫ a b f 2 x d x
Cho hàm số y=f(x) liên tục trên [a,b]. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục Ox, các đường thẳng x=a, x=b và V là thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox, khẳng định nào sau đây đúng?
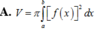
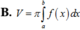
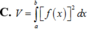
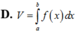
Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các đường y = f x , trục Ox và hai đường thẳng x = a , x = b xung quanh trục Ox.
A. π ∫ a b f 2 x d x
B. ∫ a b f 2 x d x
C. π ∫ a b f x d x
D. 2 π ∫ a b f 2 x d x
Cho hình phẳng (D) được giới hạn bởi các đường x = 0 , x = π , y = 0 và y = − sin x . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức:
A. V = π ∫ 0 π sin x d x .
B. V = π ∫ 0 π sin 2 x d x .
C. V = π ∫ 0 π − sin x d x .
D. V = ∫ 0 π sin 2 x d x .
Thể tích khối tròn xoay được tạo thành khi quay quanh trục Ox hình phẳng (H) được giới hạn bởi các đường y = f x liên tục trên đoạn a ; b trục Ox và hai đường thẳng x = a ; x = b là:
A. π ∫ a b f x d x
B. π ∫ b a f 2 x d x
C. ∫ a b f 2 x d x
D. π ∫ a b f 2 x d x
Cho hàm số y = f (x) liên tục trên đoạn [a;b]. Thể tích V của khối nón tròn xoay thu được khi cho hình phẳng (H) giới hạn bởi đồ thị của y = f (x), x = a, x = b (a<b) khi quay xung quanh trục Ox tính bằng công thức:
A. V = π ∫ a b f ( x ) dx
B. V = π ∫ a b f 2 ( x ) dx
C. V = π 2 ∫ a b f ( x ) dx
D. V = π ∫ a b f ( x ) dx