Thể tích vật thể tròn xoay sinh ra bởi miền CED quay quanh trục Ox là hiệu của hai thể tích ( V 1 và V 2 ) của hai vật thể tròn xoay tương ứng sinh ra khi miền ACEB và miền ACDB quay quanh trục Ox. Như vậy V = V 1 – V 2 , trong đó :

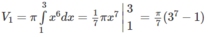
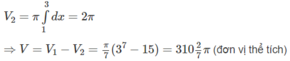
Thể tích vật thể tròn xoay sinh ra bởi miền CED quay quanh trục Ox là hiệu của hai thể tích ( V 1 và V 2 ) của hai vật thể tròn xoay tương ứng sinh ra khi miền ACEB và miền ACDB quay quanh trục Ox. Như vậy V = V 1 – V 2 , trong đó :

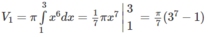
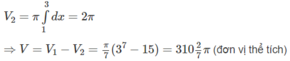
Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox: y = x α , α ∈ N*; y = 0; x = 0
Tính thể tích của vật thể tròn xoay khi quay các hình phẳng giới hạn bởi các đường sau quanh trục Ox: y = 2x/ π ; y = sinx; x ∈ [0; π /2]
Tính thể tích của vật thể tròn xoay tạo bởi khi quay quanh trục hoành Ox hình phẳng giới hạn bởi các đường thẳng y = ln x ; y = 0 ; x = 1 ; x = e
A. e - 2
B. e + 2
C. π ( e + 2 )
D. π ( e - 2 )
Cho hình phẳng (D) giới hạn bởi các đường y= x - 2 2 và y = 4. Tính thể tích của vật thể tròn xoay sinh ra bởi hình (D) khi nó quay xung quanh trục Ox
A. 118 π 5
B. 253 π 7
C. 112 π 3
D. 256 π 5
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = ln x , y = 0 , x = 2 quanh trục Ox là:
![]()
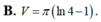
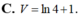
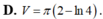
Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục Ox hình phẳng giới hạn bởi các đường y = 0 ; y = x ; y = x - 2
A. 8 π 3
B. 16 π 3
C. 10 π
D. 8 π
Thể tích vật thể tròn xoay khi cho hình phẳng (H) giới hạn bởi các đường y = x ln x y = 0 ; x = 2 quay quanh trục Ox được tính bởi công thức nào?
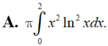
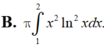
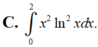
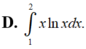
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường 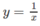 , y = 0, x = 1 và x = a (a > 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi a → +
∞
(tức là
, y = 0, x = 1 và x = a (a > 1). Gọi thể tích đó là V(a). Xác định thể tích của vật thể khi a → +
∞
(tức là 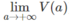 ).
).
Thể tích của khối tròn xoay tạo thành khi quay quanh trục tung hình phẳng giới hạn bởi các đường y = x , y = 2 - x và trục Ox.
A. 32 π 15
B. 12 π 15
C. 5 π 2
D. 38 π 15