Lời giải:
Gọi tổng trên là $A$
$A=2(\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.11}+...+\frac{1}{100.103})$
$A=\frac{2}{3}(\frac{3}{1.4}+\frac{3}{4.7}+\frac{3}{7.11}+...+\frac{3}{100.103})$
$=\frac{2}{3}(\frac{4-1}{1.4}+\frac{7-4}{4.7}+...+\frac{103-100}{100.103})$
$=\frac{2}{3}(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+....+\frac{1}{100}-\frac{1}{103})$
$=\frac{2}{3}(1-\frac{1}{103})$
$=\frac{2}{3}.\frac{102}{103}=\frac{68}{103}$
Bạn Akai Haruma đáp án của bạn đúng khi phân số 1/7*11 là 1/7*10
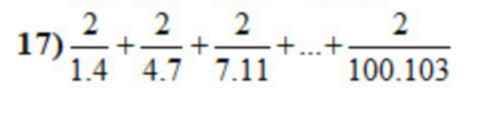

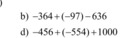 tính hợp lí nếu có thể
tính hợp lí nếu có thể