Các câu hỏi tương tự
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng
28
5
(phần gạch chéo trong hình vẽ). Diện tích hình phẳn...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x 0; x 2 có diện tích bằng
28
5
(phần gạch chéo tro...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = 0; x = 2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x = − 1 ; x = 0 có diện tích bằng:
A. 2 5 .
B. 1 9 .
C. 2 9 .
D. 1 5 .
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C), biết rằng (C) đi qua điểm
A
−
1
;
0
. Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0, x2 bằng...
Đọc tiếp
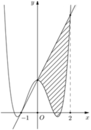
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A − 1 ; 0 . Tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2. Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0, x=2 bằng 28 5 (phần tô đậm trong hình vẽ).
Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x= -1, x=0 có diện tích bằng
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x0, x2 có diện tích bằng
28
5
(phần gạch chéo trong hình vẽ) A.
2...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0, x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ)
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số
y
f
x
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
∈
ℝ
,
a
≠
0
có đồ thị (C). Biết...
Đọc tiếp
Cho hàm số
y
=
f
x
=
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
∈
ℝ
,
a
≠
0
có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y = f '(x) cho bởi hình vẽ dưới đây.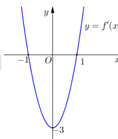
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
A. S = 9
B. S = 5 4
C. S = 21 4
D. S = 27 4
Cho Parabol
P
:
y
2
x
2
. Gọi d là tiếp tuyến với (P) tại điểm có hoành độ bằng 2. Tính diện tích hình phẳng giới hạn bởi đồ thị (P), đường thẳng d và đường thẳng x1. A.
2
3
B.
1
2
C.
1
3
D.
3
2
Đọc tiếp
Cho Parabol P : y = 2 x 2 . Gọi d là tiếp tuyến với (P) tại điểm có hoành độ bằng 2. Tính diện tích hình phẳng giới hạn bởi đồ thị (P), đường thẳng d và đường thẳng x=1.
A. 2 3
B. 1 2
C. 1 3
D. 3 2
Gọi D là hình phẳng giới hạn bởi đồ thị (C) của hàm số
y
x
4
-
2
x
2
+
1
,
tiếp tuyến D của (C) tại điểm có hoành độ x 2 và trục hoành. Quay D xung quanh trục hoành tạo thành một khối tròn xoay có thể tích V được tính theo công thức A.
V
π
∫
-
1...
Đọc tiếp
Gọi D là hình phẳng giới hạn bởi đồ thị (C) của hàm số y = x 4 - 2 x 2 + 1 , tiếp tuyến D của (C) tại điểm có hoành độ x = 2 và trục hoành. Quay D xung quanh trục hoành tạo thành một khối tròn xoay có thể tích V được tính theo công thức
A. V = π ∫ - 1 2 x 2 - 1 4 d x - 81 π 8
B. V = π ∫ - 1 2 x 2 - 1 4 d x
C. V = π ∫ 1 2 x 2 - 1 4 d x - 81 π 8
D. V = π ∫ - 1 39 24 x 2 - 1 4 d x
Cho đồ thị hàm số
f
(
x
)
x
3
+
a
x
2
+
b
x
+
c
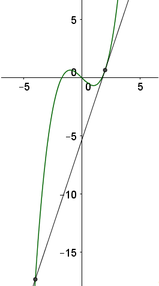
có đồ thị (C). Đừng thẳng d qua hai điểm A, B trê hình vẽ là tiếp tuyến của (C) tại A. Diện tích hình phẳng giới hạn bởi d và C bằng A. 6,575 B. 4,5 C. 8,45 D. 4,75
Đọc tiếp
Cho đồ thị hàm số f ( x ) = x 3 + a x 2 + b x + c có đồ thị (C). Đừng thẳng d qua hai điểm A, B trê hình vẽ là tiếp tuyến của (C) tại A. Diện tích hình phẳng giới hạn bởi d và C bằng
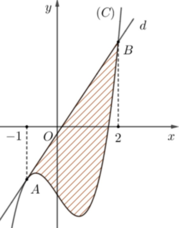
A. 6,575
B. 4,5
C. 8,45
D. 4,75
Cho hàm số
y
f
x
a
x
3
+
b
x
2
+
c
x
+
d
có đồ thị (C). Biết rằng đường thẳng
y
-
9
là tiếp tuyến của (C) tại điểm có hoành độ dương và đồ thị của
y...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 2 + c x + d có đồ thị (C). Biết rằng đường thẳng y = - 9 là tiếp tuyến của (C) tại điểm có hoành độ dương và đồ thị của y = f x được cho như hình vẽ. Diện tích hình phẳng giới hạn bởi (C) và trục hoành có số đo gần nhất với số nào dưới đây?
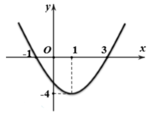
A.
B. 29,25
C. 31,5
D. 35,15