Các câu hỏi tương tự
Cho hàm số f(x)=ln2018-ln(x+1 / x).Tính S=f’(1)+f’(2)+f’(3)+…+f’(2017)
A. 4035 2018
B. 2017
C. 2016 2017
D. 2017 2018
Đạo hàm của hàm số
y
x
+
2
x
-
1
ln
(
x
+
2
)
là A.
y
2
x
log
(...
Đọc tiếp
Đạo hàm của hàm số y = x + 2 x - 1 ln ( x + 2 ) là
A. y ' = 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
B. y ' = x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
C. y ' = 2 x log ( 2 x - 1 ) + 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
D. y ' = - 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
Cho hàm số f(x)3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số
y
f
3
(
x
)
-
3
mf
2
(
x
)
+
3
(
m...
Đọc tiếp
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Gọi S là tập hợp tất cả các giá trị thực của a sao cho đường thẳng ya(x-1)-3 cắt đồ thị (C) của hàm số
y
2
x
3
-
3
x
2
-
2
tại ba điểm M,N,P(1;-3) và tiếp tuyến của (C) tại M,N vuông góc với nhau. Tổng các phần tử của S bằng A. -1. B. 1. C. 2. D. -2
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của a sao cho đường thẳng y=a(x-1)-3 cắt đồ thị (C) của hàm số y = 2 x 3 - 3 x 2 - 2 tại ba điểm M,N,P(1;-3) và tiếp tuyến của (C) tại M,N vuông góc với nhau. Tổng các phần tử của S bằng
A. -1.
B. 1.
C. 2.
D. -2
Gọi S là tập hợp các số nguyên m để hàm số
y
f
(
x
)
x
+
2
m
-
3
x
-
3
m
+
2
đồng biến trên khoảng (-∞;-14) . Tính tổng T của các phần tử trong S A. T-10 B. T-9...
Đọc tiếp
Gọi S là tập hợp các số nguyên m để hàm số y = f ( x ) = x + 2 m - 3 x - 3 m + 2 đồng biến trên khoảng (-∞;-14) . Tính tổng T của các phần tử trong S
A. T=-10
B. T=-9
C. T=-6
D. T=-5
Cho hàm số
y
f
(
x
)
x
3
+
a
x
2
+
b
x
+
c
đạt cực tiểu bằng – 3 tại điểm x1 và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính đạo hàm cấp một của hàm số tại x -3 A. f(-3) 0 B. f(-3) 2 C. f(-3) 1 D. f(-3) -2
Đọc tiếp
Cho hàm số y = f ( x ) = x 3 + a x 2 + b x + c đạt cực tiểu bằng – 3 tại điểm x=1 và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính đạo hàm cấp một của hàm số tại x= -3
A. f'(-3)= 0
B. f'(-3)= 2
C. f'(-3)= 1
D. f'(-3)= -2
Cho hàm số yf(x) liên tuc trên R và thỏa mãn f(0)0f(-1) Gọi S là diện tích hình phẳng giới hạn bởi các đường
y
f
x
,
y
0
,
x
−
1
v
à
x
1.
Xét các mênh đề sau
1.
S
∫
−
1...
Đọc tiếp
Cho hàm số y=f(x) liên tuc trên R và thỏa mãn f(0)<0<f(-1) Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f x , y = 0 , x = − 1 v à x = 1. Xét các mênh đề sau
1. S = ∫ − 1 0 f x d x + ∫ 0 1 f x d x 2. S = ∫ − 1 1 f x d x 3. S = ∫ − 1 1 f x d x 4. S = ∫ − 1 1 f x d x
Số mệnh đề đúng là
A. 2
B. 1
C. 3
D. 4
Cho hàm số yf(x) có đạo hàm là
f
(
x
)
(
x
−
1
)
2
(
x
+
2
)
3
(
3
−
x
)
. Khi đó số điểm cực trị của hàm số là A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm là
f ' ( x ) = ( x − 1 ) 2 ( x + 2 ) 3 ( 3 − x ) . Khi đó số điểm cực trị của hàm số là
A. 0
B. 1
C. 2
D. 3
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = - 2017 ( x - 1 ) ( x + 2 ) 3 ( x - 3 ) 2 Tìm số điểm cực trị của f(x)
A. 3
B. 2
C. 0
D. 1
Cho hàm số
y
f
x
có đạo hàm liên tục trên R và có đồ thị của hàm số
y
f
x
như hình vẽ bên dưới.Để hàm số
y
f
2
x
3
-
6
x
+
3...
Đọc tiếp
Cho hàm số y = f x có đạo hàm liên tục trên R và có đồ thị của hàm số y = f ' x như hình vẽ bên dưới.
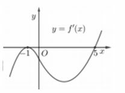
Để hàm số y = f 2 x 3 - 6 x + 3 đồng biến với mọi x > m m ∈ R thì m ≥ a sin b π c , trong đó a , b , c ∈ N * , c > 2 b . Tổng S = 2a + 3b -c bằng
A. – 9
B. 7
C. 5
D. -2

