1 2 2 ln 6 - 2 6 + 2
Hướng dẫn: Đặt t = x + 1/x, ta nhận được:
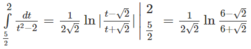
1 2 2 ln 6 - 2 6 + 2
Hướng dẫn: Đặt t = x + 1/x, ta nhận được:
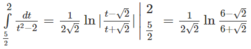
Tính các tích phân sau: 1) 2 ln e e x dx ; 2) 1 3 2 0 4 x dx x ; 3) /2 /4 1 tan dx x ; 4) 1 0 x e dx ; 5) 2 1 x xe dx ; 6) 0 1 3 4 dx x ; 7) 2 1 4 4 5 dx x x ; 8) 2 0 ln 1 x dx x (HD: 1 u x ) ĐS: 1) 2 e ; 2) 16 7 5 3 ; 3) ln 2 ; 4) 2
Tính các tích phân sau bằng phương pháp đổi biến số: ∫ 1 2 x 1 - x 5 d x (đặt t = 1 - x)
Tính tích phân I=\(\int\limits^{\pi}_0\)\(x^2cos2xdx\) bằng cách đặt \(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\).Mệnh đề nào dưới đây đúng?
A. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-\int\limits^{\pi}_0xsin2xdx\)
B. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-2\int\limits^{\pi}_0xsin2xdx\)
C. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+\int\limits^{\pi}_0xsin2xdx\)
D. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+2\int\limits^{\pi}_0xsin2xdx\)
Từ phương trình ( 3 + 2 2 ) x - 2 ( 2 - 1 ) x = 3 đặt t = ( 2 - 1 ) x ta thu được phương trình nào sau đây?
A. t 3 - 3 t - 2 = 0
B. 2 t 3 + 3 t 2 - 1 = 0
C. 2 t 3 + 3 t - 1 = 0
D. 2 t 2 + 3 t - 1 = 0
Tính diện tích hình phẳng giới hạn bởi các đường sau:
a) y = 2x – x 2 , x + y = 2 ;
b) y = x 3 – 12x, y = x 2
c) x + y = 1, x + y = -1, x – y = 1, x – y = -1;
d) 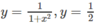
e) y = x 3 – 1 và tiếp tuyến với y = x 3 – 1 tại điểm (-1; -2).
Tính các tích phân sau: ∫ 2 5 4 + x x d x (Đặt t = 4 + x )
Tìm a để hai đường thẳng sau đây cắt nhau: d : x = 1 + a t y = t z = - 1 + 2 t d ' : x = 1 - t ' y = 2 + 2 t ' z = 3 - t '
Tính các tích phân sau: ∫ - 3 2 d x x + 7 + 3 (đặt t = x + 7 hoặc t = x + 7 + 3)
Xét tính hội tụ phân kỳ của tích phân:
I = \(\int\limits^{+\text{∞}}_1\dfrac{x^2-1}{x^4+1}dx\)