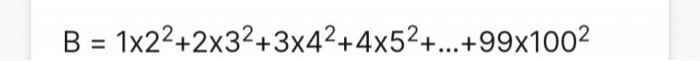\(B=1.2^2+2.3^2+...+99.100^2\\=(2-1).2^2+(3-1).2^2+(100-1).100^2\\=2^3-2^2+3^3-3^2+...+100^3-100^2\\ =(2^3+3^3+...+100^3)-(2^2+3^2+...+100^3)\\ =(1^3+2^3+3^3+...+100^3)-(1^2+2^2+3^2+...+100^3)\\ =\dfrac{[100.(100+1)]^2}{4}-\dfrac{100.(100+1).(2.100+1)}{6} =25164150\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Viết biểu thức tính viết biểu thức tính diện tích hình thang có đáy bé là a đáy lớn là b chiều cao là h tính giá trị biểu thức đó với a = 13 cm b = 17 cm h = 15cm
Cho biểu thức: (a+b-c)-(a-b+c) a) Thu gọn biểu thức trên b) Tính giá trị biểu thức với a=5, b=7, c=8
Câu 3: Tính giá trị của biểu thức C = 5a − 4b + 7a + 8 . Biết a-b=8.
Câu 4: Tính giá trị của biểu thức D =4a + 10b - b+ 2a. Biết 2a+3b=12
Câu 5: Tính giá trị của biểu thức D=21a + 9b — 6a — 4b. Biết 3a+b=18
Câu 3: Tính giá trị của biểu thức C 5a − 4b + 7a + 8 . Biết a-b8.
Câu 4: Tính giá trị của biểu thức D 4a + 10b - b+ 2a. Biết 2a+3b12
Câu 5: Tính giá trị của biểu thức D21a + 9b — 6a — 4b. Biết 3a+b18
Đọc tiếp
Câu 3: Tính giá trị của biểu thức C = 5a − 4b + 7a + 8 . Biết a-b=8.
Câu 4: Tính giá trị của biểu thức D =4a + 10b - b+ 2a. Biết 2a+3b=12
Câu 5: Tính giá trị của biểu thức D=21a + 9b — 6a — 4b. Biết 3a+b=18
1.1. Tính giá trị biểu thức: 1.1. Tính giá trị biểu thức: 1.1. Tính giá trị biểu thức: 1.1. Tính giá trị biểu thức: 1.1. Tính giá trị biểu thức: 1.1. Tính giá trị biểu thức: vdn1.1. Tính giá trị biểu thức:
Đọc tiếp
1.1. Tính giá trị biểu thức:
1.1. Tính giá trị biểu thức: ![]() 1.1. Tính giá trị biểu thức:
1.1. Tính giá trị biểu thức: ![]()
1.1. Tính giá trị biểu thức:
1.1. Tính giá trị biểu thức: ![]()
1.1. Tính giá trị biểu thức: ![]()
vdn1.1. Tính giá trị biểu thức: ![]()
cho biểu thức A=(x-1)2 -3
a, tính giá trị của biểu thức A với x=-2
b, tính giá trị biểu thức nhỏ nhất của biểu thức A
1. Cho biểu thức A= (x-1)^2-3.
a. tính giá trị của biểu thức A với x = -2 b. tính giá trị nhỏ nhất của biểu thức ATính GTNN của biểu thức
a) A= 3 + |x|
b) B= |x-5|+5
Tính GTLN của biểu thức
a) A= 3 - |x +1|
b) B= -4 - |3 - x|
Cho biểu thức B= 2x +y – 5x + 2y
Rút gon biểu thức B
Tính giá trị của B tại X = oy = -1
a,Tính giá trị nhỏ nhất của biểu thức A=|x-100|-101
b,Tính giá trị nhỏ nhất của biểu thức A= -|x+101|-100