Các câu hỏi tương tự
a = (sqrt(20001) - sqrt(19999))/(sqrt(20001) + sqrt(19999)) + (sqrt(20001) + sqrt(19999))/(sqrt(20001) - sqrt(19999))
Đề bài là tính a ạ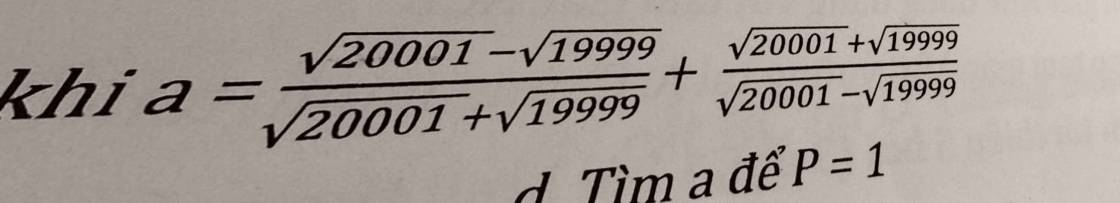 
cho P= \(\left(\dfrac{a+\sqrt{a}}{\sqrt{a}+1}+1\right)\) \(.\left(\dfrac{a-\sqrt{a}}{\sqrt{a}-1}-1\right)\) . \(\dfrac{2-\sqrt{2}}{\sqrt{2}-1}\)
a, đkxđ
b,rút tính gọn
c,tính gtbt tại a = \(\sqrt{2+\sqrt{2}}\)
Tính
a) \(\sqrt{6-\sqrt{11}}\cdot\sqrt{6+\sqrt{11}}\)
b) \(\sqrt{8+\sqrt{15}}\cdot\sqrt{8-\sqrt{15}}\)
thực hiện phép tính ( rút gọn biểu thức )
a) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{\sqrt{a}+\sqrt{b}}{a-b}\)
b) \(\dfrac{a-b}{\sqrt{a}+\sqrt{b}}-\dfrac{a-2\sqrt{ab}+b}{\sqrt{a}-\sqrt{b}}\)
P = ((sqrt(a) + 1)/(sqrt(a) - 1) - (sqrt(a) - 1)/(sqrt(a) + 1) + 4sqrt(a))(sqrt(a) - 1/(sqrt(a))) a) Rút gọn P. b) Tính giá trị của P tại a = (2 + sqrt(3))(sqrt(3) - 1) * sqrt(2 - sqrt(3))
tính \(A=\left(\frac{\sqrt{a}+1}{\sqrt{a}-1}-\frac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right)\left(\sqrt{a}+\frac{1}{\sqrt{a}}\right)\)
a) rút gọn A
b) tính A với \(a=\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\left(\sqrt{4-\sqrt{15}}\right)\)
1. Tính A= \(\dfrac{2+\sqrt{3}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}+\dfrac{2-\sqrt{3}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}\)
TM
22 tháng 3 2022 lúc 8:36
Thực hiện các phép tính :
1. \(A=\sqrt{2-\sqrt{3}}\sqrt{2+\sqrt{2-\sqrt{3}}}\sqrt{2+\sqrt{2+\sqrt{2-\sqrt{3}}}}\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2-\sqrt{3}}}}}\)
2. \(B=\left(\dfrac{1}{1+\sqrt{2}}+\dfrac{2}{2+\sqrt{3}}+...+\dfrac{1}{20+\sqrt{21}}\right)\cdot2022\)
Giải chi tiết giúp mình ạ
Tính
a) \(\dfrac{2}{\sqrt{3}-\sqrt{5}}+\dfrac{3-2\sqrt{3}}{\sqrt{3}-2}\)
b) \(\dfrac{5-\sqrt{5}}{\sqrt{5}-1}+\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}\)