Chọn A
Phương trình hoành độ giao điểm
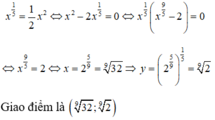
Chọn A
Phương trình hoành độ giao điểm
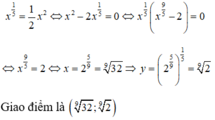
Tọa độ giao điểm của đồ thị các hàm số:
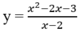
và y = x + 1 là:
A. (2; 2); B. (2; -3);
C(-1; 0); D. (3; 1).
Trong không gian Oxyz, cho đường thẳng
d: x - 1 - 1 = y + 3 2 = z 1 và cho mặt phẳng
(P): 2x + y - 2z + 9 = 0. Tọa độ giao điểm của d và (P) là
![]()
![]()
![]()
![]()
Tọa độ giao điểm của đồ thị các hàm số: y = x 2 - 2 x - 3 x - 2
và y = x + 1 là:
A. (2; 2); B. (2; -3);
C(-1; 0); D. (3; 1).
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3-3( m+1) x2+ 12mx-3m+ 4 ( C) có hai điểm cực trị là A và B sao cho hai điểm này cùng với điểm C(-1; -9/2) lập thành tam giác nhận gốc tọa độ làm trọng tâm.
A. m= -1/2
B. m= -2
C. m=2
D. m =1/2
Tìm tọa độ giao điểm của đồ thị của mỗi cặp hàm số sau: y = 1 3 x và y = 9
Số giao điểm của đồ thị hàm số y = (x − 3)( x 2 + x + 4) với trục hoành là:
A. 2; B. 3;
C. 0; D. 1.
Số giao điểm của đồ thị hàm số y = (x − 3)( x 2 + x + 4) với trục hoành là:
A. 2; B. 3;
C. 0; D. 1
Tìm điểm cận đứng và điểm cận ngang của hàm số sau
1) y= 2+1/x+2
2) y= 2+1/1-x
3) y= x^2-9/x-3
4) y= 2x-1+1/x