Đáp án là B.
Đặt t = x - 2 x Đạo hàm t , = 1 + 2 x 2 > 0
Do đó t ( 1 ) ≤ t ≤ t ( 2 ) , ∀ x ∈ [ 1 ; 2 ] , suy ra - 1 ≤ t ≤ 1
Ta có x 2 + 4 x 2 = t 2 + 4 , x 4 + 16 x 4 = ( x 2 + 4 x 2 ) 2 - 8 = ( t 2 + 4 ) 2 - 8 = t 4 + 8 t 2 + 8
Phương trình đã cho trở thành
t 4 + 8 t 2 + 8 - 4 ( t 2 + 4 ) - 12 t = m ⇔ t 4 + 4 t 2 - 12 t = m + 8 ( * )
Phương trình đã cho có nghiệm trong đoạn [1;2] khi và chỉ khi phương trình (*) có nghiệm trong [-1;1] Xét hàm số y=f(t)= t 4 + 4 t 2 - 12 t trên [-1;1]
Đạo hàm y , = 4 t 8 + 8 t - 12 , t ∈ ( - 1 ; 1 ) . y , = 4 ( t - 1 ) ( t 2 + t + 3 ) < 0 , ∀ t ∈ ( - 1 ; 1 )
Bảng biến thiên:
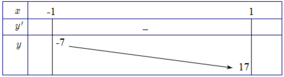
Do đó để phương trình đã cho có nghiệm trên [1;2] thì - 7 ≤ m + 8 ≤ 17 ⇔ - 15 ≤ m ≤ 9