Chọn A
Ta có:
![]()
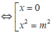
Hàm số (C) có ba điểm cực trị ⇔ m ≠ 0 (*) .
Với điều kiện (*) gọi ba điểm cực trị là:
![]() .
.
Do đó nếu ba điểm cực trị tạo thành một tam giác vuông cân, thì sẽ vuông cân tại đỉnh A.
Do tính chất của hàm số trùng phương, tam giác ABC đã là tam giác cân rồi, cho nên để thỏa mãn điều kiện tam giác là vuông, thì AB vuông góc với AC
![]()
Tam giác ABC vuông khi:
![]()
![]()
![]()
Vậy với m = ± 1 thì thỏa mãn yêu cầu bài toán.
[Phương pháp trắc nghiệm]
Yêu cầu bài toán
⇔ b 3 8 a + 1 = 0 ⇔ - m 6 + 1 = 0
⇔ m = ± 1

