Đạo hàm y’ = 3x2 – 3m
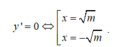
Hàm số có 2 cực trị khi và chỉ khi : m> 0
Khi đó tọa độ 2 điểm cực trị của đồ thị hàm số là:
M ( m ; - 2 m m + 2 ) N ( - m ; 2 m m + 2 ) ⇒ M N → = ( - 2 m ; 4 m m )
Phương trình đường thẳng MN: 2mx+ y-2=0
Ta có :
S ∆ I A B = 1 2 I A . I B . sin A I B ^ = 1 2 sin A I B ^ ≤ 1 2
Dấu bằng xảy ra khi
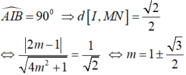
Chọn B.

