Đáp án B
Điều kiện để đồ thị có tiệm cận: ![]()
Tâm đối xứng I(1;-m) là giao điểm của hai đường tiệm cận.
Khi đó, ![]() (loại). Vậy không tồn tại m thỏa mãn.
(loại). Vậy không tồn tại m thỏa mãn.
Đáp án B
Điều kiện để đồ thị có tiệm cận: ![]()
Tâm đối xứng I(1;-m) là giao điểm của hai đường tiệm cận.
Khi đó, ![]() (loại). Vậy không tồn tại m thỏa mãn.
(loại). Vậy không tồn tại m thỏa mãn.
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C) , đường thẳng (d): y=m(x+1) với m là tham số, đường thẳng ∆ : y = 2 x - 7 . Tìm tổng tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại 3 điểm phân biệt A(-1;0); B;C sao cho B,C cùng phía với ∆ và d B ; ∆ + d C ; ∆ = 6 5 .
A. 0
B. 8
C. 5
D. 4
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y = 2 x - 3 ( m - 1 ) x 2 + 4 có tiệm cận ngang
A. m > 0
B. m ≥ 1
C. m > 1
D. Không có giá trị nào của m
Cho hàm số y = 1 x 3 - 3 x 2 + m - 1 với m là tham số. Tìm tất cả các giá trị của m để đồ thị hàm số đã cho có 4 đường thẳng tiệm cận.
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x - 2 x 2 - m x + 1 có đúng 3 đường tiệm cận.
A. -2<m<2
B. m > 2 m < - 2 h o ặ c m ≠ - 5 2
C. m>2 hoặc m<-2
D. m > 2 m ≠ 5 2 hoặc m<-2
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số ( C m ) : y = x - 1 x 2 + x - m có hai đường tiệm cận đứng.
A. Mọi ![]()
B. 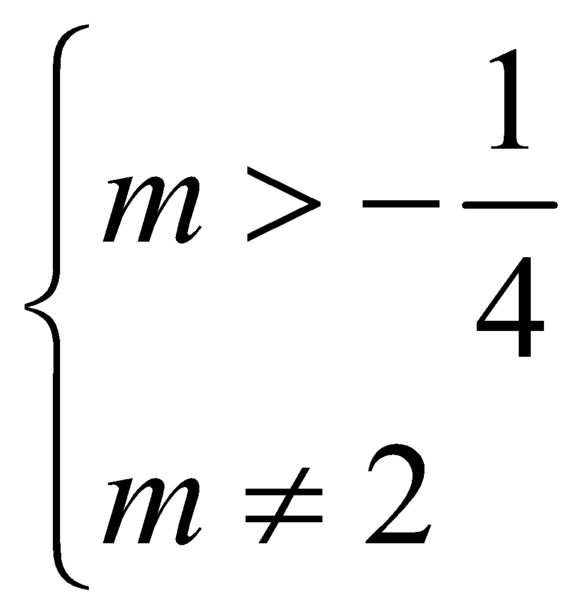
C. 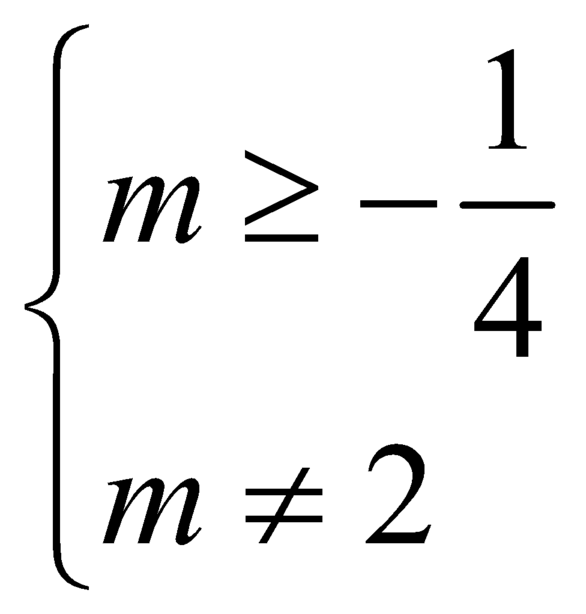
D. ![]()
Tìm tất cả giá trị của m để đồ thị hàm số y = x 2 + x - 2 x 2 - 2 x - m có 3 đường tiệm cận
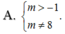
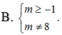
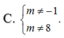
![]()
Cho hàm số y = f(x) = 1 x 3 - 3 x 2 + m - 1 . Tìm tất cả các giá trị của m để đồ thị hàm số có 4 đường thẳng tiệm cận.
A. 1 < m < 5
B. -1 < m < 2
C. m < -1; m > 2
D. m < 1; m > 5
Tìm tất cả các giá trị của tham số m sao cho đồ thị (Cm) của hàm số y = 2 x + m x m + 1 có tiệm cận đứng, tiệm cận ngang và các tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8.
A.![]()
B. ![]()
C. ![]()
D. không có m thỏa mãn.
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = x + 1 m x 2 + 1 có hai tiệm cận ngang
A. m < 0
B. m = 0
C. m > 0
D. Không có giá trị thực của m