Chọn A
Điều kiện xác định của hàm số là ![]()
Chọn A
Điều kiện xác định của hàm số là ![]()
Có bao nhiêu giá trị nguyên của m thuộc khoảng (-2019;2019) để hàm số sau có tập xác định là D = ℝ
y = x + m + x 2 + 2 ( m + 1 ) x + m 2 + 2 m + 4 + log 2 ( x - m + 2 x 2 + 1 )
A. 2020
B. 2021
C. 2018
D. 2019
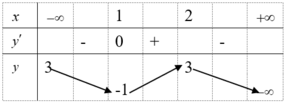
Hàm số y=f(x) có bảng biến thiên ở bên. Trong các phát biểu dưới đây có bao nhiêu phát biểu đúng?
(*): y = 3 là tiệm cận ngang
(*): Tập xác định D = ℝ / 2
(*): Max y = 3 (*): Min y = -1
(*): x C Đ = 2
![]()
![]()
![]()
![]()
Tìm tập xác định D của hàm số y = ( 2 - x ) 1 - 3
![]()
![]()
![]()
![]()
Tìm tập xác định D của hàm số y = l n ( 1 - x ) 2
![]()
![]()
![]()
![]()
Tìm tập xác định D của hàm số y = l o g ( x 2 - x - 2 ) (1)
![]()
![]()
![]()
![]()
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8
Tìm tập xác định của D của hàm số y = (x2 - 1)-2.
![]()
![]()
![]()
![]()
Hàm số y = log 2 ( 4 x - 2 x + m ) có tập xác định là D = ℝ khi
A . m ≤ 1 4
B . m ≥ 1 4
C . m > 1 4
D . m < 1 4
Cho hàm số y = f x xác định trên D = ℝ \ - 2 ; 2 , liên tục trên mỗi khoảng xác định và có bảng biến thiên sau
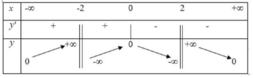 Có bao nhiêu khẳng định đúng trong các khẳng định sau?
Có bao nhiêu khẳng định đúng trong các khẳng định sau?
(I). Đồ thị hàm số có 2 tiệm cận.
(II). Hàm số đạt giá trị lớn nhất bằng 0.
(III). Hàm số có đúng 1 điểm cực trị.
(IV). Đồ thị hàm số có 3 tiệm cận.
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = ( m - 1 ) x 3 - 3 ( m + 2 ) x 2 - 6 ( m + 2 ) x + 1 . Tập giá trị của m để y ' ≥ 0 ∀ x ∈ ℝ là
A. [3;+ ∞ )
B. ∅
C. [ 4 2 ;+ ∞ )
D. [1;+ ∞ )