Chọn A.
Ta có: f’(x) = 3x2 – 6x.
f’(x) < 0 ⇔ 3x2 – 6x < 0 ⇔ 0 < x < 2.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
LV
9 tháng 5 2021 lúc 20:47
Cho f(x)=1/3(m-1)x³-mx²+(m+2)x-5. Tìm m để a)f'(x) lớn hơn hoặc bằng 0 với mọi x b)f'(x) nhỏ hơn hoặc bằng 0 với mọi x c)f'(x)=0 có 2 nghiệm cùng âm d)f'(x)=0 có nghiệm thỏa mãn x1+2x2=1
Cho hàm số
f
x
x
3
.
sin
1
x
k
h
i
x
≠...
Đọc tiếp
Cho hàm số f x = x 3 . sin 1 x k h i x ≠ 0 0 k h i x = 0 . Đạo hàm f’(x) là biểu thức nào sau đây?
A.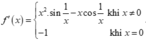 
B. 
C.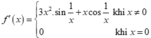 
D.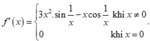 
Tính đạo hàm của hàm số
f
(
x
)
x
3
-
2
x
2
+
x
+...
Đọc tiếp
Tính đạo hàm của hàm số f ( x ) = x 3 - 2 x 2 + x + 1 - 1 x - 1 k h i x ≢ 1 0 k h i x = 1 tại điểm x 0 = 1
A. 1 3
B. 1 5
C. 1 2
D. 1 4
Tìm a để hàm số
f
(
x
)
5
a
x
2
+
3
x
+
2
a
+
1
k...
Đọc tiếp
Tìm a để hàm số f ( x ) = 5 a x 2 + 3 x + 2 a + 1 k h i x ≥ 0 1 + x + x 2 + x + 2 k h i x < 0 có giới hạn tại x → 0
A. +∞
B. -∞
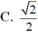
D. 1
Cho hàm số
f
(
x
)
3
-
4
-
x
4
k
h
i
x...
Đọc tiếp
Cho hàm số f ( x ) = 3 - 4 - x 4 k h i x ≢ 0 1 4 k h i x = 0 . Khi đó đạo hàm của hàm số tại điểm x = 0 là kết quả nào sau đây?
A. 1 4
B. 1 16
C. 1 32
D. Không tồn tại
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
1) đạo hàm của hàm số \(\dfrac{2x^2+1}{x^2}\) là
2) cho hàm số \(f\left(x\right)=\sqrt{-5x^2+14x-9}\) tập hợp các giá trị của x để f'(x) = 0 là
Cho hàm số
f
x
x
2
n
ế
u
x
≥
0
x
2
...
Đọc tiếp
Cho hàm số f x = x 2 n ế u x ≥ 0 x 2 - 1 n ế u x < 0
a) Vẽ đồ thị của hàm số f(x). Từ đó dự đoán về giới hạn của f(x) khi x → 0
b) Dùng định nghĩa chứng minh định nghĩa trên
Cho hàm số y = f ( x ) = - x 3 - 3 x 2 + 9 x + 2011 có đồ thị (C). Giải bất phương trình: f'(x) ≤ 0.