Chọn B
Đặt t = 1 + x ⇒ x = ( t - 1 ) 2 ⇒ d x = 2 t - 1 d t
Khi đó
∫ 1 1 + x d x = ∫ 2 ( t - 1 ) t d t = 2 ∫ 1 - 1 t d t = 2 ( t - ln t ) + C 1 = 2 x + 1 - ln 1 + x + C 1 = 2 x - 2 ln 1 + x + C
(Với C = 2 + C 1 và 1 + x > 0 )
Chọn B
Đặt t = 1 + x ⇒ x = ( t - 1 ) 2 ⇒ d x = 2 t - 1 d t
Khi đó
∫ 1 1 + x d x = ∫ 2 ( t - 1 ) t d t = 2 ∫ 1 - 1 t d t = 2 ( t - ln t ) + C 1 = 2 x + 1 - ln 1 + x + C 1 = 2 x - 2 ln 1 + x + C
(Với C = 2 + C 1 và 1 + x > 0 )
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số f x = 1 1 + sinx
a) F(x) = 1 - cos x 2 + π 4
b) G(x) = 2 tan x 2
c) H(x) = ln(1 + sinx)
d) K(x) = 2 1 - 1 1 + tan x 2
Giả sử F(x) là một nguyên hàm của f ( x ) = ln ( x + 3 ) x 2 sao cho F(-2)+F(1)=0. Giá trị của F(-1)+F(2) bằng
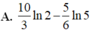
B. 0
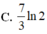
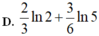
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F(0) = –ln2. Tìm tập nghiệm S của phương trình F(x) + ln(ex + 1) = 3.
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3
Họ nguyên hàm của hàm số f(x) = 4x(1+ln x) là
A. 2 x 2 ln x + 3 x 2
B. 2 x 2 ln x + x 2
C. 2 x 2 ln x + 3 x 2 + C
D. 2 x 2 ln x + x 2 + C
Cho hàm số f ( x ) = ln 2019 - ln x + 2 x tính tổng S = f ' ( 1 ) + f ' ( 3 ) + . . . + f ' ( 2019 )
A. 4305 2019
B. 2021
C. 2019 2021
D. 2020 2021
Họ các nguyên hàm của hàm số f(x) = (2x + 1) ln x là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Biết F ( x ) là một nguyên hàm của hàm số f ( x ) = ln 2 x + 1 . ln x x thoả mãn F ( 1 ) = 1 3 . Giá trị của F 2 ( e ) là
A. 8 9
B. 1 9
C. 8 3
D. 1 3
Họ nguyên hàm của hàm số f(x) = 2x ( 2 + ln x) là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x ) .
Tập nghiệm của bất phương trình
f ( a - 1 ) + f ( ln a ) ≤ 0 là:
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) liên tục trên khoảng 0 ; + ∞ . Biết f(1) = 1 và f(x) = xf'(x) + ln (x). Giá trị f(e) bằng
A. e
B. 1
C. 2
D. 1 e