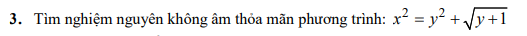\(x^2+6y^2=2015-7xy\\ \Leftrightarrow x^2+xy+6xy+6y^2=2015\\ \Leftrightarrow x\left(x+y\right)+6y\left(x+y\right)=2015\\ \Leftrightarrow\left(x+6y\right)\left(x+y\right)=2015\\ =1\cdot\left(-2015\right)=\left(-1\right)\cdot2015\\ =-5\cdot403=5\left(-403\right)\\ =65\cdot\left(-31\right)=-65\cdot31\\ =13\cdot\left(-155\right)=-13\cdot155\)
Thay vào lần lượt rồi ra.