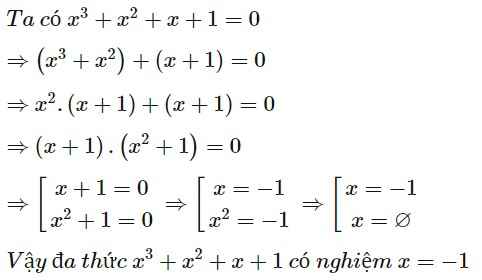Cho `f(x)=0`
`=>x^3+x^2+x+1=0`
`=>x^2(x+1)+(x+1)=0`
`=>(x+1)(x^2+1)=0`
Mà `x^2+1 > 0`
`=>x+1=0`
`=>x=-1`
Vậy nghiệm của đa thức `f(x)` là `x=-1`
Xét \(f\left(x\right)=x^3+x^2+x+1\)
\(\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow x=-1\) do \(x^2+1>0\)
Vậy tập nghiệm của đa thức \(f\left(x\right)\) là \(S=\left\{-1\right\}\)