Question

Tìm m để hàm số y = - 2x^2- (2m - 1)x + 6 - 3m nghịch biến trong khoảng (-2 ; dương vô cùng)

Answer 1

 Xét parabol \(\left(C_m\right):y=-2x^2-\left(2m-1\right)x+6-3m\), ta có \(\Delta=\left[-\left(2m-1\right)\right]^2-4\left(-2\right)\left(6+3m\right)=4m^2+20m+49\)

  Gọi \(I_m\) là đỉnh của \(\left(C_m\right)\) thì \(I_m\left(\dfrac{-2m+1}{4};\dfrac{4m^2+20m+49}{8}\right)\)

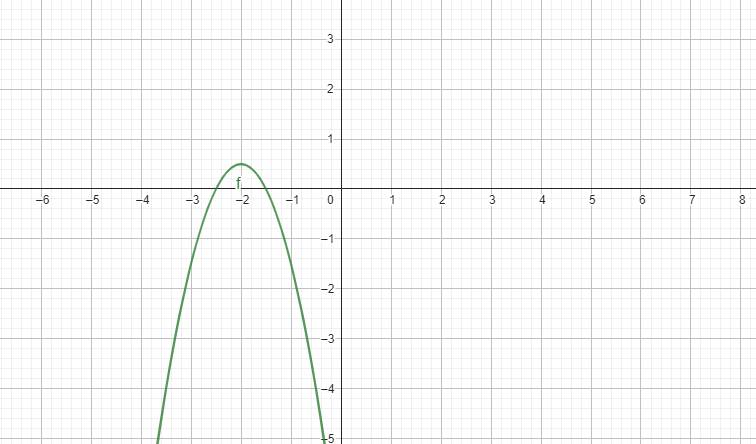
  Để hàm số đã cho nghịch biến trong khoảng \(\left(-2;+\infty\right)\) thì \(\dfrac{-2m+1}{4}=-2\Leftrightarrow m=\dfrac{9}{2}\)

 

Answer 2

Tao đéo biết thằng Nguyễn Huy Hung nha ☹

Answer 3

Để hàm số nghịch biến trên \(\left(-2;+\infty\right)\)

\(\Rightarrow\left(-2;+\infty\right)\subset\left(\dfrac{1-2m}{4};+\infty\right)\)

\(\Rightarrow\dfrac{1-2m}{4}\ge-2\)

\(\Rightarrow m\le\dfrac{9}{2}\)