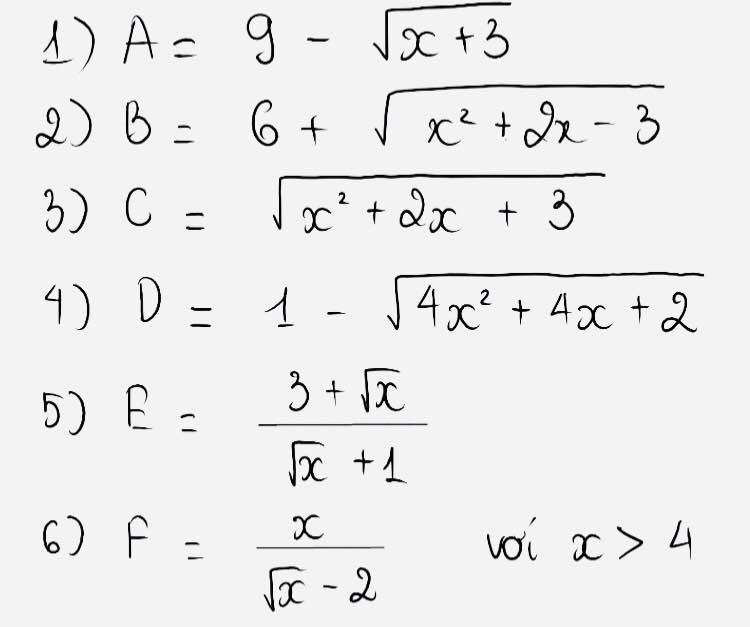\(N=\sqrt{\dfrac{x^2}{4}+\sqrt{x^2-4}}+\sqrt{\dfrac{x^2}{4}-\sqrt{x^2-4}}\)
\(=\dfrac{1}{2}\left(\sqrt{x^2+4\sqrt{x^2-4}}+\sqrt{x^2-4\sqrt{x^2-4}}\right)\)
\(=\dfrac{1}{2}\left[\sqrt{x^2-4+4\sqrt{x^2-4}+4}+\sqrt{x^2-4-4\sqrt{x^2-4}+4}\right]\)
\(=\dfrac{1}{2}\left[\sqrt{\left(\sqrt{x^2-4}+2\right)^2}+\sqrt{\left(\sqrt{x^2-4}-2\right)^2}\right]\)
\(=\dfrac{1}{2}\left[\left|\sqrt{x^2-4}+2\right|+\left|2-\sqrt{x^2-4}\right|\right]\)
Ta có : |a| + |b| \(\ge\left|a+b\right|\) . Khi đó : \(N\ge\dfrac{1}{2}\left|\sqrt{x^2-4}+2+2-\sqrt{x^2-4}\right|=2\)
" = " \(\Leftrightarrow\left(\sqrt{x^2-4}+2\right)\left(2-\sqrt{x^2-4}\right)=0\)
\(\Leftrightarrow\sqrt{x^2-4}=2\) \(\Leftrightarrow x^2-4=4\Leftrightarrow x^2=8\)
\(\Leftrightarrow x=\pm2\sqrt{2}\)
Vậy ...
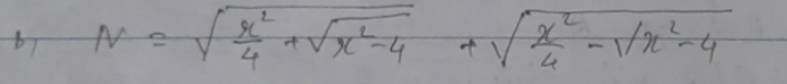 tìm gtnn
tìm gtnn