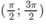\(y=\dfrac{sinx+1}{sin^2x+sinx+1}\)
Ta thấy :
\(-1\le sinx\le1\)
\(\Rightarrow\left\{{}\begin{matrix}0\le sinx\le2\\sin^2x+sinx+1>0\left(\Delta=-3< 0;a=1>0\right)\end{matrix}\right.\)
\(\Rightarrow0\le y=\dfrac{sinx+1}{sin^2x+sinx+1}\le2\)
\(\Rightarrow\left\{{}\begin{matrix}Min\left(y\right)=0\left(x=\dfrac{3\pi}{2}+k2\pi\right)\\Max\left(y\right)=2\left(x=\dfrac{\pi}{2}+k2\pi\right)\end{matrix}\right.\)
\(y=\dfrac{sinx+1}{sin^2x+sinx+1}\left(1\right)\). Đặt \(t=sinx\left(t\in\left[-1;1\right]\right)\).
Để ý \(y\ge0,\forall x\in R\)
-Với \(t=-1\left(x=-\dfrac{\pi}{2}+k2\pi\right)\) thì \(y=0\)
-Với \(t\ne-1\), khi đó \(y\ne0\). Từ (1) ta có: \(yt^2+yt+y=t+1\)
\(\Rightarrow yt^2+\left(y-1\right)t+\left(y-1\right)=0\) (*)
Xét phương trình (*) là phương trình bậc 2 ẩn t tham số y.
Để phương trình (*) có nghiệm thì: \(\Delta\ge0\)
\(\Leftrightarrow\left(y-1\right)^2-4y\left(y-1\right)\ge0\)
\(\Leftrightarrow-3y^2+2y+1\ge0\) \(\Leftrightarrow-\dfrac{1}{3}\le y\le1\) \(\Rightarrow0\le y\le1\)
Phương trình (*) nếu có nghiệm kép thì nghiệm kép là \(t_0=\dfrac{1-y}{2y}\). Khi đó \(\Delta=0\Leftrightarrow y=1\Leftrightarrow t=0\Leftrightarrow x=k\pi\).
Vậy \(\left\{{}\begin{matrix}Miny=0\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\\Maxy=1\Leftrightarrow x=k\pi\end{matrix}\right.\)
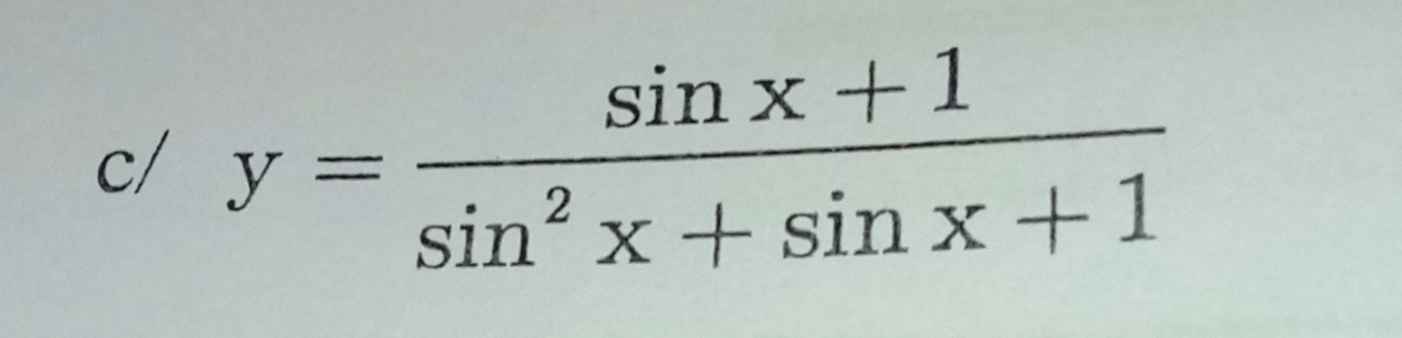
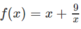
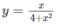trên khoảng (−
∞
;+
∞
);
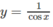trên khoảng 