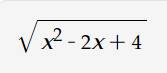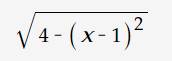Question

Tìm giá trị lớn nhất của biểu thức

Answer 1

ĐK: `x >= 0`

Ta có: `x-2\sqrt{x}+2=x-2\sqrt{x}+1+1=(\sqrt{x}-1)^2+1`

Với `x >= 0<=>(\sqrt{x}-1)^2 >= 0`

                `<=>(\sqrt{x}-1)^2+1 >= 1`

                `<=>1/[(\sqrt{x}-1)^2+1] <= 1`

           Hay `1/[x-2\sqrt{x}+2] <= 1`

Dấu "`=`"xảy ra `<=>(\sqrt{x}-1)^2=0<=>x=1` (t/m)

Vậy `GTLN` của bth là `1` khi `x=1`

Answer 2

\(\dfrac{1}{x-2\sqrt{x}+1+1}=\dfrac{1}{\left(x-1\right)^2+1}\)

Để biểu thức đạt GTLN thì \(\left(x-1\right)^2+1\) đạt GTNN

Ta có: \(\left(x-1\right)^2\ge0\)

⇔ \(\left(x-1\right)^2+1\ge1\)

Dấu = xảy ra khi \(\left(x-1\right)^2=0\Leftrightarrow x=1\)

Vậy GTLN của biểu thức là 1 khi \(x=1\)