Vì \(\alpha\in\left\{\dfrac{\pi}{2};\dfrac{3\pi}{2}\right\}\Rightarrow cos\alpha< 0\)
\(sin2\alpha=2sin\alpha cos\alpha=-\dfrac{4}{5}\Rightarrow sin\alpha cos\alpha=-\dfrac{4}{5}:2=-\dfrac{2}{5}\left(1\right)\)
\(sin^2\alpha+cos^2\alpha=1\\ \Rightarrow sin^2\alpha+cos^2\alpha+2sin\alpha cos\alpha=1+2sin\alpha cos\alpha\\ \Rightarrow\left(sin\alpha+cos\alpha\right)^2=1-\dfrac{4}{5}\)
\(\Rightarrow\left(sin\alpha+cos\alpha\right)^2=\dfrac{1}{5}\)
\(\Rightarrow sin\alpha+cos\alpha=\dfrac{1}{\sqrt{5}}\left(2\right)\)
Gọi \(x_1,x_2\) lần lượt là \(sin\alpha,cos\alpha\)
Từ \(\left(1\right),\left(2\right)\)\(\Rightarrow\left\{{}\begin{matrix}x_1x_2=-\dfrac{2}{5}\\x_1+x_2=\dfrac{1}{\sqrt{5}}\end{matrix}\right.\)
Ta có pt \(x^2-\dfrac{1}{\sqrt{5}}x-\dfrac{2}{5}=0\) hay \(x^2+\dfrac{1}{\sqrt{5}}x-\dfrac{2}{5}=0\)
Giải hệ ta được \(x_1=\dfrac{2}{\sqrt{5}};x_2=-\dfrac{1}{\sqrt{5}}\) hay \(x_1=\dfrac{1}{\sqrt{5}};x_2=-\dfrac{2}{\sqrt{5}}\)
\(\Rightarrow sin\alpha=\dfrac{2}{\sqrt{5}};cos\alpha=-\dfrac{1}{\sqrt{5}}\left(tmdk\right)\) hay \(sin\alpha=\dfrac{1}{\sqrt{5}};cos\alpha=-\dfrac{2}{\sqrt{5}}\left(tmdk\right)\)
Vậy ...
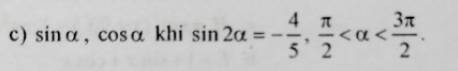



 .
.