y = x 3 - 3 x 2 − 24x + 7. TXĐ: R
y′ = 3 x 2 − 6x – 24 = 3( x 2 − 2x − 8)
y′ = 0 ⇔ 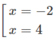
Vì y′′(−2) = −18 < 0, y′′(4) = 18 > 0 nên hàm số đạt cực đại tại x = -2; đạt cực tiểu tại x = 4 và y CĐ = y(-2) = 35; y CT = y(4) = -73.
y = x 3 - 3 x 2 − 24x + 7. TXĐ: R
y′ = 3 x 2 − 6x – 24 = 3( x 2 − 2x − 8)
y′ = 0 ⇔ 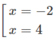
Vì y′′(−2) = −18 < 0, y′′(4) = 18 > 0 nên hàm số đạt cực đại tại x = -2; đạt cực tiểu tại x = 4 và y CĐ = y(-2) = 35; y CT = y(4) = -73.
Tìm cực trị của các hàm số sau: y = (7 - x) x + 5 3
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số y = 3 x - 2 5 - x là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
y
=
3
x
2
-
2
x
+
5
x
2
+
x
+
7
Câu 7 : Tìm tập hợp tất cả các giá trị của m để hàm số \(y=x^3+\left(3m-1\right)x^2+m^2x-3\) đạt cực tiểu tại x=-1
Cho hàm số y = x 3 - 2 x 2 - 1 (1) và các mệnh đề
(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3
(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3
(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3
(4) Cực trị của hàm số (1) là x = 0 và x = 4/3
Trong các mệnh đề trên, số mệnh đề sai là:
A. 0
B. 1
C. 2
D. 3
Tìm các điểm cực trị và các giá trị cực trị của hàm số \(y = \sqrt{2x-x^3}\)
Câu 3: Tìm tất cả các giá trị của tham số m để hàm số \(y=x^3-3x^2+mx+1\) đạt cực tiểu tại x=2
Cho hàm số y = x 3 - 6 x 2 + 3 ( m + 2 ) x - m - 6 . Tìm tất cả các giá trị thực của m để hàm số có 2 cực trị cùng dấu
A. - 23 4 < m < 2 .
B. - 15 4 < m < 2 .
C. - 21 4 < m < 2 .
D. - 17 4 < m < 2 .