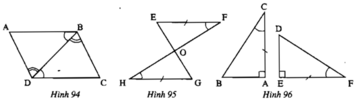
-Hình 94:
ΔABD và ΔCDB có
∠(ABD) = ∠(BDC) (gt)
BD cạnh chung
∠(ADB) = ∠(DBC)
Nên ΔABD = ΔCDB (g.c.g)
-Hình 95
Ta có: ∠(EFO) + ∠(FEO) + ∠(EOF) = ∠(GHO) + ∠(HGO) + ∠(GOH) = 180o
∠(EFO) = ∠(GHO) (Gt)
∠(EOF) = ∠(GOH) (hai góc đối đỉnh)
⇒ ∠(FEO) = ∠(HGO)
ΔEOF và ΔGOH có
∠(EFO) = ∠(OHG) (gt)
EF = GH (gt)
∠(FEO) = ∠(HGO) (CMT)
Nên ΔEOF = ΔGOH (g.c.g)
-Hình 96
ΔABC và ΔEDF có
∠(BAC)= ∠(DEF) (gt)
AC = EF
∠(ACB) = ∠(EFD)
Nên ΔABC = ΔEDF (g.c.g)