Chọn A
Tập xác định: D = (0; +∞)
y' ≥ 0 ⇔ lnx ≤ 1 ⇔ 0 ≤ x ≤ e
Từ bảng xét dấu của y’ ta thấy hàm số đồng biến trên (0; e).
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Tìm khoảng đồng biến của hàm số yln(x-1) A. B. C. D.
Đọc tiếp
Tìm khoảng đồng biến của hàm số y=ln(x-1)
A.
B. 
C. 
D. 
Cho bốn hàm số sau : y f(x) lnx ;
y
g
(
x
)
2
x
2
+
4
;
y
h
(
x
)
2017
1018
x
và y l(x) ln( x2+1). Có bao nhiêu hàm số...
Đọc tiếp
Cho bốn hàm số sau : y= f(x) = lnx ; y = g ( x ) = 2 x 2 + 4 ; y = h ( x ) = 2017 1018 x và
y= l(x)= ln( x2+1). Có bao nhiêu hàm số đồng biến trên khoảng ( 0 ; + ∞ )
A. 1
B. 2
C. 3
D. 4
PP
5 tháng 8 2023 lúc 10:07
Câu 22. Cho hàm số yf(x)��(�) có đạo hàm trên khoảng (a;b)(�;�). Tìm mệnh đề sai trong các mệnh đề sau.A. Nếu hàm số yf(x)��(�) đồng biến trên (a;b)(�;�) thì f′(x)0�′(�)0 với mọi x∈(a;b)�∈(�;�).B. Nếu hàm số yf(x)��(�) nghịch biến trên (a;b)(�;�) thì f′(x)≤0�′(�)≤0 với mọi x∈(a;b)�∈(�;�).C. Nếu f′(x)0�′(�)0 với mọi x∈(a;b)�∈(�;�) thì hàm số yf(x)��(�) đồng biến trên (a;b)(�;�).D. Nêu f′(x)0�′(�)0 với mọi x∈
Đọc tiếp
Câu 22. Cho hàm số có đạo hàm trên khoảng . Tìm mệnh đề sai trong các mệnh đề sau.A. Nếu hàm số đồng biến trên thì với mọi .B. Nếu hàm số nghịch biến trên thì với mọi .C. Nếu với mọi thì hàm số đồng biến trên .D. Nêu với mọi
Cho hàm số y f(x) liên tục trên khoảng
0
;
+
∞
. Biết f(1) 1 và f(x) xf(x) + ln (x). Giá trị f(e) bằng A. e B. 1 C. 2 D.
1
e
Đọc tiếp
Cho hàm số y = f(x) liên tục trên khoảng 0 ; + ∞ . Biết f(1) = 1 và f(x) = xf'(x) + ln (x). Giá trị f(e) bằng
A. e
B. 1
C. 2
D. 1 e
Tìm các khoảng đồng biến của hàm số
y
x
-
x
4
,
x 0 A.
0
;
1
16
B.
0
;
1
4
C.
1
16...
Đọc tiếp
Tìm các khoảng đồng biến của hàm số y = x - x 4 , x > 0
A. 0 ; 1 16
B. 0 ; 1 4
C. 1 16 ; + ∞
D. 1 4 ; + ∞
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
Hàm số
y
-
x
4
2
+
1
đồng biến trên khoảng:A. (-
∞
; 0); B. (1; +
∞
);C. (-3; 4); D. (-
∞
; 1).
Đọc tiếp
Hàm số y = - x 4 2 + 1 đồng biến trên khoảng:
A. (- ∞ ; 0); B. (1; + ∞ );
C. (-3; 4); D. (- ∞ ; 1).
Cho hàm số
y
f
x
xác định, có đạo hàm trên đoạn
a
;
b
(với
a
b
). Xét các mệnh đề sau: i) Nếu
f
x...
Đọc tiếp
Cho hàm số y = f x xác định, có đạo hàm trên đoạn a ; b (với a < b ). Xét các mệnh đề sau:
i) Nếu f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên khoảng a ; b .
ii) Nếu phương trình f ' ( x ) = 0 có nghiệm x 0 thì f ' ( x ) đổi dấu từ dương sang âm khi qua x 0 .
iii) Nếu f ' x ≤ 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
Số mệnh đề đúng trong các mệnh đề trên là:
A. 2
B. 3
C. 0
D. 1
Cho hàm số
f
x
a
x
5
+
b
x
4
+
c
x
3
+
d
x
2
+...
Đọc tiếp
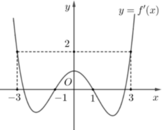
Cho hàm số f x = a x 5 + b x 4 + c x 3 + d x 2 + e x + f với a, b, c, d, e, f là các số thực; đồ thị của y = f ' x như hình vẽ bên. Hàm số y = f 1 - 2 x - 2 x 2 + 1 đồng biến trên khoảng nào dưới đây?
A. - 3 2 ; - 1
B. - 1 2 ; 1 2
C. (-1;0)
D. (1;3)
Hàm số y = x 2 e - x tăng trong khoảng:
A. (- ∞ ;0) B. (2; + ∞ )
C. (0;2) D. (- ∞ ; + ∞ )