Tập xác định D = [0; 1]
Ta có:
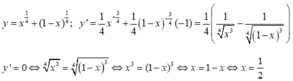
y(0) = y(1) = 1; y 1 2 = 8 4 . Từ đó max m a x y = 8 4 , m i n y = 1 , min y = y(0) = 1
Chọn C
Tập xác định D = [0; 1]
Ta có:
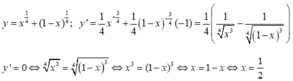
y(0) = y(1) = 1; y 1 2 = 8 4 . Từ đó max m a x y = 8 4 , m i n y = 1 , min y = y(0) = 1
Chọn C
Tính tổng tất cả các giá trị của m biết đồ thị hàm số y = x 3 - 2 mx 2 + ( m + 2 ) x + 4 và đường thẳng y = x + 4 cắt nhau tại 3 điểm phân biệt A(0;4), B, C sao cho diện tích tam giác IBC bằng 8 2 với I(1;3)
A.3
B. 8
C. 1
D. 5
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x - 2 + 4 - x lần lượt là M và m. Chọn câu trả lời đúng.
A. M = 4, m = 2
B. M = 2, m = 0
C. M = 3, m = 2
D. M = 2, m = 2
Cho z là số phức thay đổi thỏa mãn ( 1 + i ) z + 2 - i = 4 và M(x,y) là điểm biểu diễn cho z trong mặt phẳng phức. Tìm giá trị lớn nhất của biểu thức T = x + y + 3
A. T = 4 + 2 2
B. 8
C. 4
D. 4 2
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Trong không gian Oxyz cho mặt cầu ( S ) : ( x - 4 ) 2 + ( y - 2 ) 2 + ( z - 4 ) 2 = 1 . Điểm M(a;b;c) thuộc (S). Tìm giá trị nhỏ nhất của a 2 + b 2 + c 2
A. 25
B. 29
C. 24
D. 26
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Gọi M, N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x + 4 - x 2 . Giá trị của biểu thức (M + 2N) là
A. 2 2 + 2
B. 4 - 2 2
C. 2 2 - 4
D. 2 2 - 2
Gọi M; N lần lượt là giá trị nhỏ nhất, lớn nhất của hàm số y = ln ( x + x 2 + 4 ) trên đoạn [0;5] Khi đó tổng M+N là
A. ![]()
B. 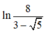
C. ![]() .
.
D. Kết quả khác
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x - 4 - x 2 Tính tổng M+m
A. 2 - 2
B. 2 1 + 2
C. 2 1 - 2
D. 4