Chọn đáp án B
Hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành là nghiệm của phương trình :
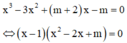
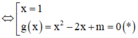
Để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục hoành
Phương trình (*) có hai nghiệm phân biệt khác 1
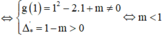
Chọn đáp án B
Hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành là nghiệm của phương trình :
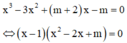
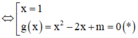
Để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục hoành
Phương trình (*) có hai nghiệm phân biệt khác 1
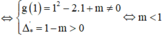
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 3 - m + 1 x 2 + m 2 - 2 x - m 2 + 3 có hai điểm cực trị và hai điểm cực trị đó nằm về cùng một phía đối với trục hoành?
A. 4
B. 1
C. 3
D.
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 3 − 8 x 2 + ( m 2 + 11 ) x - 2m 2 + 2 có hai điểm cực trị nằm về hai phía của trục Ox.
A. 4
B. 5
C. 6
D. 7
Tìm các giá trị thực của tham số m sao cho đồ thị hàm số y = 1 3 x 3 − 3 m x 2 + m có các điểm cực đại và cực tiểu nằm về hai phía của trục hoành.
A. 0 < m < 1 6 .
B. m ≠ 0 .
C. m > 1 6 .
D. m < 1 6 .
Cho hàm số y = x 3 + 3 m x 2 − m có đồ thị (C). Tất cả các giá trị của tham số thực m để (C) có hai điểm cực trị nằm về cùng một phía so với trục hoành là
A. m < − 1 2 h o ặ c m > 1 2
B. − 1 2 < m < 1 2 v à m ≠ 0
C. 0 < m < 1 2
D. − 1 2 < m ≤ 0
Tập hợp tất cả các giá trị của tham số m để đồ thị hàm số y = x 3 + 3 m x 2 + 3 m 2 - 1 x + m 3 có hai điểm cực trị nằm về hai phía trục hoành khoảng (a,b). Giá trị của a+ 2b bằng
A. 4/3
B. 3/2
C. 1
D. 2/3
Có bao nhiêu giá trị nguyên của m để đồ thị hàm số y = x 3 - 5 2 x 2 - 2 x + 1 - m có hai điểm cực trị nằm về hai phía trục hoành?
A. 6.
B. 4.
C. 5.
D. 3.
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 1 3 x 3 − m − 1 x 2 + m − 1 x + m 2 có hai điểm cực trị nằm về phía bên phải trục tung.
A. m < 0
B. m < 1
C. m > 2
D. m > 0
Cho hàm số y = x 3 + 1 − 2 m x 2 + 2 2 − m x + 4. Với giá trị nào của tham số m thì đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục hoành?
A. m > 2 m < − 2 .
B. − 2 < m < 2.
C. m ≥ 2 − 5 2 ≠ m ≤ − 2 .
D. m > 2 − 5 2 ≠ m < − 2 .
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số y = 1 3 x 3 − x 2 + m − 1 x + 2 có hai điểm cực trị đều nằm bên trái trục tung.
A. 1 < m < 2
B. m > 1
C. m < 2
D. m < 1